Bài 90, 91 trang 54 SBT Toán 7 tập 2

Bài 90, 91 trang 54 SBT Toán 7 tập 2

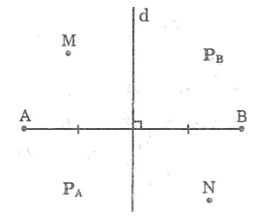
Bài 90: Đường trung trực d của đoạn thẳng AB chia mặt phẳng thành hai phần (không kể đường thẳng d): phần chứa điểm A ký hiệu là P_A, phần chứa điểm B ký hiệu là P_B (hình bên).

a. Gọi M là một điểm của P_A. Chứng minh rằng MA < MB

b. Gọi N là một điểm của P_B. Chứng minh rằng NB < NA

c. Gọi K là một điểm sao cho KA < KB. Hỏi rằng K nằm ở đâu: trong P_A, P_B hay trên d?

Lời giải:

a. Nối MA, MB. Gọi C là giao điểm của MB với đường thẳng d, nối CA.

Ta có: MB = MC + CB

mà CA = CB (tính chất đường trung trực)

Suy ra: MB = MC + CA    (1)

Trong ΔMAC ta có:

MA < MC + CA (bất đẳng thức tam giác)    (2)

Từ (1) và (2) suy ra: MA < MB

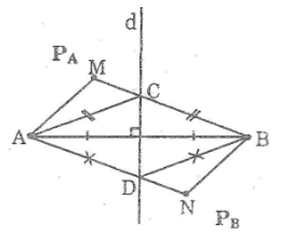
b. Nối NA, NB. Gọi D là giao điểm của NA với đường thẳng d, nối DB.

Ta có: NA = ND + DA

mà DA = DB (tính chất đường trung trực)

Suy ra: NA = ND + DB    (3)

Trong ΔNDB, ta có:

NB < ND + DB (bất đẳng thức tam giác)    (4)

Từ (3) và (4) suy ra: NA > NB

c. Theo câu a), ta có: MA < MB

Mà M là một điểm của P_A nên K là một điểm của P_A.

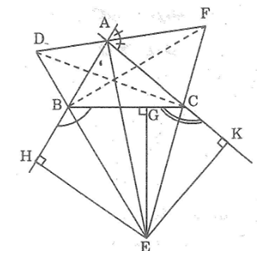
Bài 91: Cho tam giác ABC, các đường phân giác của các góc ngoài tại B và C cắt nhau ở E. Gọi G, H, K theo thứ tự là chân đường vuông góc kẻ từ E đến các đường thẳng BC, AB, AC.

a. Có nhận xét gì về các độ dài EH, EG, EK?

b. Chứng minh AE là tia phân giác của góc BAC.

c. Đường phân giác của góc ngoài tại A của tam giác ABC cắt các đường thẳng BE, CE tại D, F. Chứng minh rằng EA vuông góc với DF.

d. Các đường thẳng AE, BF, CD là các đường gì trong tam giác ABC?

e. Các đường thẳng EA, FB, DC là các đường gì trong tam giác DEF?

Lời giải:

a. Ta có: E thuộc tia phân giác của ∠(CBH)

Suy ra: EG = EH (tính chất tia phân giác)    (1)

    E thuộc tia phân giác của ∠(BCK)

Suy ra: EG = EK (tính chất tia phân giác)    (2)

Từ (1) và (2) suy ra: EH = EG = EK.

b. Ta có: EH = EK (chứng minh trên)

Suy ra: E thuộc tia phân giác của ∠(BAC).

Mà E khác A nên AE là tia phân giác của ∠(BAC)

c. Ta có: AE là tia phân giác góc trong tại đỉnh A

    AF là tia phân giác góc trong tại đỉnh A

Suy ra: AE ⊥ AF (tính chất hai góc kề bù)

Vậy AE ⊥ DF.

d. Tương tự câu a, ta có:

    BF là tia phân giác của ∠(ABC)

    CD là tia phân giác của ∠(ACB)

Vậy AE, BF, CD là các đường phân giác của tam giác ABC.

e. Ta có: BF là tia phân giác góc trong tại đỉnh B

    BE là tia phân giác góc trong tại đỉnh B

Suy ra: BF ⊥ BE (tính chất hai góc kề bù)

Vậy BF ⊥ ED.

Lại có: CD là đường phân giác góc trong tại C

    CE là đường phân giác góc trong tại C

Suy ra: CD ⊥ CE (tính chất hai góc kề bù)

Vậy CD ⊥ EF.