Cho hai tam giác vuông cân OAB VÀ O’A’B’ có chung đỉnh O

Bài 4: Phép quay và phép đối xứng tâm

Bài 13 (trang 18 sgk Hình học 11 nâng cao): Cho hai tam giác vuông cân OAB VÀ O’A’B’ có chung đỉnh O sao cho O nằm trên đoạn thẳng AB’ và nằm ngoài đoạn thẳng A’B. GỌI G và G’ lần lượt là trọng tâm của tam giác OAA’ và OBB’. Chứng minh GOG’ là tam giác vuông cân

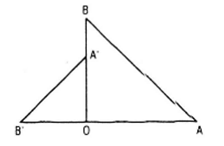
Lời giải:

Gọi Q là phép quay tâm O , góc quay π/2 (bằng góc lượng giác (OA,OB))

Khi đó Q biến A thành B và biến A’ thành B’ , tức là biến tam giác OAA’ thành tam giác OBB’

Bởi vậy Q biến G (trọng tâm tam giác OAA’) thành G’(trọng tâm tam giác OBB’). Suy ra OG = OG’ và GÔG' = π/2

Vậy GOG’ là tam giác vuông cân tại đỉnh O.

Chú ý : Phép quay Q biến trọng tâm tam giác ABC thành trọng tâm G’ của tam giác A’B’C’ ảnh của ΔABC qua Q được suy từ phép quay Q biến trung điểm I của đoạn thẳng AB thành trung điểm I’ của đoạn thẳng A’B’ ảnh của AB qua Q.