Chứng tỏ rằng các đa giác đều có cùng số cạnh thì đồng dạng với nhau

Bài 7: Phép đồng dạng

Bài 32 (trang 31 sgk Hình học 11 nâng cao): Chứng tỏ rằng các đa giác đều có cùng số cạnh thì đồng dạng với nhau

Lời giải:

Giả sử cho hai n-giác đều A₁A₂...A_n và B₁B₂…B_n có tâm lần lượt là O và O'. Đặt :

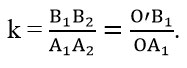
Gọi V là phép vị tự tâm O , tỉ số k và C₁C₂…C_n là ảnh của đa giác A₁A₂…A_n qua phép vị tự V . Hiển nhiên C₁C₂…C_n cũng là đa giác đều vì :

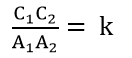
Nên C₁C₂ = B₁B₂. Vậy hai n-giác đều C₁C₂….C_n và B₁B₁…B_n có cạnh bằng nhau, tức là có phép dời hình D biến C₁C₂…C_n thành B₁B₂…B_n (xem BT22, chương I, SGK). Nếu gọi F là phép hợp thành của V và D thì F là phép đồng đạng biến A₁A₂…A_n thành B₁B₂…B_n.Vậy hai đa giác đều đó đồng dạng với nhau