Cho lăng trụ ABC.A’B’C. Gọi H là trung điểm của canh A’B’

Bài 4: Hai mặt phẳng song song

Bài 36 (trang 68 sgk Hình học 11 nâng cao): Cho lăng trụ ABC.A’B’C. Gọi H là trung điểm của canh A’B’.

a) Chứng minh rằng đường thẳng CB’ song song với mp(AHC’)

b) Tìm giao tuyến d của hai mp(A’B’C’) và (A’BC). Chứng minh rằng d song song với mp(BB’C’C)

c) Xác định thiết diện của hình lăng trụ ABC. A’B’C’ khi cắt bởi mp(H, d).

Lời giải:

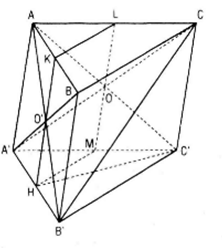
a) Chứng minh CB’// (AHC’) ta tìm trong(AHC’) một đường thẳng song song với CB’ , muốn vậy ta tìm giao điểm của một mặt phẳn chứA CB’ với (AHC’) đó là (A’C’B’). Gọi O là giao điểm AC và A’C.AA’C’C là hình bình hành nên O là trung điểm của A’C

Do đó HO là đường trung bình của ΔA’B’C’

⇔ HO // BC ⇒ BC // (AHC’)

(Vì HO ⊂ (AHC’) )

b) Tìm giao tuyến d của (A’B’C’) và (A’BC)

Gọi O là giao điểm của AB’ và A’B thì O, O’ là hai điểm chung của hai mặt phẳng

(AB’C’) và (A’BC) nên : (AB’C’) ∩ (A’BC) = OO’

Vậy d = OO’. Ta có O’ là trung điểm của AB’(vì AA’B’B là hình bình hành)

⇔ OO’ là đường trung bình của ΔAB’C’

⇔ OO’ // B’C’// BC ⇒ OO’// (BB’C’C)⇒ d // (BB’C’C)

c) Gọi {K} = HO’ ∩ AB thì HK // AA’

Qua O kẻ ML// AA’(M Є A’C’, L Є AC). Thiết diện cần tìm là hình bình hành HKLM