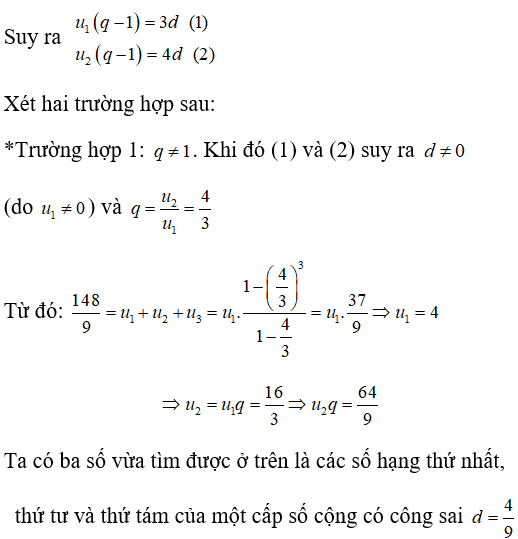Hãy tìm 3 số hạng đầu tiên của một cấp số nhân, biết rằng tổng của chúng bằng

Luyện tập (trang 121)

Bài 42 (trang 122 sgk Đại Số và Giải Tích 11 nâng cao): Hãy tìm 3 số hạng đầu tiên của một cấp số nhân, biết rằng tổng của chúng bằng 148/9 và đồng thời các số hạng đó tương ứng là số hạng đầu, số hạng thứ 4 và số hạng thứ tám của một cấp số cộng.

Lời giải:

Kí hiệu u₁, u₂, u₃ lần lượt là số hạng thứ nhất, thứ hai , thứ ba của cấp số nhân nói trong đề bài; gọi q là công bội của cấp nhân đó.

Gọi d là công sai của cấp số cộng nhận u₁, u₂, u₃ tương ứng là số hạng thứ nhất, thứ tư và thứ tám.

Ta có u₁ ≠ 0 , vì nếu ngược lại thì u₂ = u₃ = 0 và do đó : u₁ + u = u₁₂ + u₃ = 0 ≠ 148/9

Từ các giả thiết của đề bài ta có: u₂ = u₁.q = u₁ + 3d và u₃ = u₂.q = u₂ + 4d