Cho mp(P) và ba điểm khôg thẳng hàng A, B, C cùng nằm ngoài (P)

Bài 1: Đại cương về đường thẳng và mặt phẳng

Bài 5 (trang 50 sgk Hình học 11 nâng cao): Cho mp(P) và ba điểm khôg thẳng hàng A, B, C cùng nằm ngoài (P) . Chứng minh rằng nếu ba đường thẳng AB, BC, CA đều cắt mp (P) thì các giao điểm đó thẳng hàng.

Lời giải:

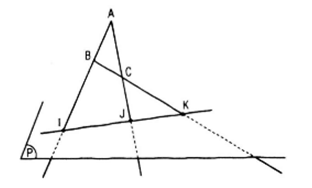
Gọi I, J, K lần lượt là giao điểm của AB, AC, BC với mp(P). A, B, C không thẳng hàng nên có mp (ABC)

Rõ ràng I, J, K Є mp(ABC) và I, J, K Є mp(P) nên I, J, k nằm trên giao tuyến của hai mp(P) và (ABC).

Vậy I, J, K thẳng hàng.