Chứng minh rằng mặt phẳng đi qua K, song song với AB và SC thì đi qua điểm N

Bài tập ôn cuối năm

Bài 7 (trang 125 sgk Hình học 11 nâng cao): Cho hình chóp S.ABC. Gọi K và N lần lượt là trung điểm của SA VÀ BC; M là điểm nằm giữa S và C

a) Chứng minh rằng mặt phẳng đi qua K, song song với AB và SC thì đi qua điểm N

b) Xác định thiết diện của hình chóp S.ABC khi cắt bởi mp(KMN). Chứng tỏ rằng KN chia thiết diện thành hai phần có diện tích bằng nhau.

Lời giải:

a) Gọi I và J lần lượt là trung điểm của SB và SC thì dễ thấy các điểm K, I , N, J cùng thuộc mặt phẳng song song với AB và SC. Vậy câu a) được chứng minh.

b) Nếu M là trung điểm của SC thì thiết diện của hình chóp S.ABC khi cắt bởi mp(MKN) là hình bình hành , trong đó P là trùng điểm của AB . Khi đó KN chia hình bình hành MKPN thành hai phần có diện tích bằng nhau.

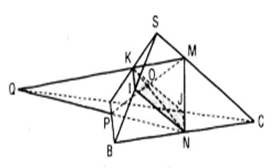
Nếu M không là trung điểm của SC. Gọi Q là giao điểm của KM và AC, P là giao điểm của QN và AB. Khi đó thiết diện của hình chóp S.ABC cắt bởi mp(MKN) là tứ giác MKPN.

Ta có : SC // (α) và AB // (α) đồng thời K là trung điểm SA nên :

d(M, (α)) = d(P, (α)) ⇒ OP = OM (với O là giao điểm của PM và NK).

Do đó hai đường cao của hai tam giác MKN và PKN kẻ từ M và P bằng nhau, từ đó suy ra S_PKN = S_MKN.