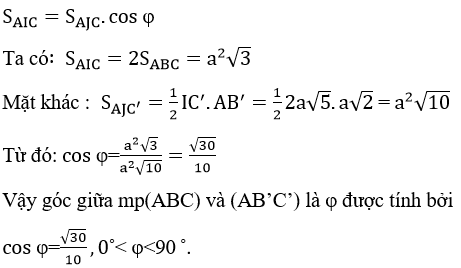Với giá trị nào của m thì AB’C’ là tam giác vuông

Bài tập ôn cuối năm

Bài 9 (trang 126 sgk Hình học 11 nâng cao): Cho tam giác ABC vuông tại A , AB = a, BC = 2a. Hai tia Bx và Cy cùng vuông góc với mp(ABC) và nằm về một phía đối với mặt phẳng đó . Trên Bx, Cy lần lượt lấy các điểm B’, C’ sao cho BB’ = a, CC’ = m.

a) Với giá trị nào của m thì AB’C’ là tam giác vuông?

b) Khi tam giác AB’C’ vuông tại B’, kẻ AH ⊥ BC. Chứng minh rằng B’C’H là tam giác vuông, tính góc giữa hai mp(ABC) và mp(AB’C’).

Lời giải:

Ta có AC²=3a²; AB'²=2a²; AC'²= 3a²+ m²; B'C'²= 4a²+ (m-a)²

a)- Tam giác AB’C’ vuông ở A khi và chỉ khi :

5a²+m²-2ma=2a²+3a²+m²

Vậy ΔAB’C’ vuông ở A khi và chỉ khi m = 0

- Tam giác AB’C’ vuông ở C’ khi và chỉ khi :

2a²= 3a²+m²+ 4a²+ (m-a)² .Điều này không xảy ra.

- Tam giác AB’C’ vuông ở B’ khi và chỉ khi :

2a²+4a²+ (m-a)² = 3a²+m² ⇔ m=2a

Vậy tam giác AB’C’ vuông ở B’ khi và chỉ khi m = 2a.

b) Giả sử tam giác AB’C’ vuông ở B’ tức là m = 2a.

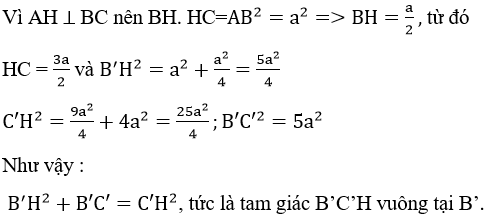
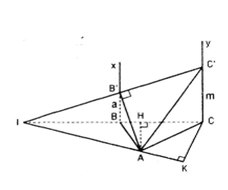
+ Tính góc giữa mp(ABC) và mp(AB’C’) khi m=2a

Gọi I là giao điểm của B’C’ và BC. Do BB’ // CC’ , BB’ = a, CC’ = 2a nên BC = BI, B’C’ = B’I.

Xét phép chiếu lên mp(ABC) . Ta có tam giác AIC là hình chiếu của tam giác AIC’. Gọi φ là góc giữa mp(ABC) và mp(AB’C’) thì :