Tính khoảng cách giữa đường thẳng AB và SC

Bài tập ôn cuối năm

Bài 8 (trang 126 sgk Hình học 11 nâng cao): Cho hình chóp đều S.ABCD có cạnh đáy bằng a và cạnh bên bằng a√2

a) Tính khoảng cách từ S đến mp(ABCD)

b) Tính khoảng cách giữa đường thẳng AB và mp(SCD)

c) Tính khoảng cách giữa đường thẳng AB và SC

d) Gọi (P) là mặt phẳng đi qua A và vuông góc với SC. Hãy xác định thiết diện của hình chóp khi cắt bởi (P). Tính diện tích thiết diện.

e) Tính góc giữa đường thẳng AB và mp(P)

Lời giải:

Gọi H là giao điểm của AC và BD . Do S.ABCD là hình chóp đều nên SH vuông góc với mặt đáy (ABCD).

a) Khoảng cách từ S đến mp(ABCD) là AH

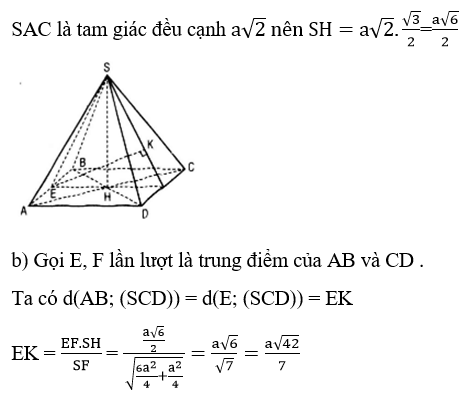
c) Vì AB và SC chéo nhau, AB // mp(SCD) nên d(AB; SC)=d(AB; (SCD))= (a√42)/7

d) Gọi C1 là trung điểm của SC, do SAC là tam giác đều nên AC₁ ⊥ SC. Mặt khác BD ⊥ SC, nên (P) chính là mặt phẳng chứa AC₁ và song song với BD. Kí hiệu H₁ là giao điểm của AC₁ và SH. Khi đó (P) ∩ (SBD) = B₁D₁, trong đó B₁D₁ đi qua H₁ và song song với BD. Vậy thiết diện của S.ABCD cắt bởi (P) là tứ giác AB₁C₁D₁

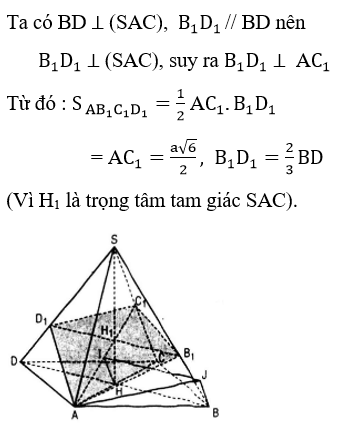
e) Trong mp(SAC) kẻ HI song song với CC₁ cắt AC₁ taị I thì HI ⊥ (P) vì SC ⊥ (P)

Ta lấy điểm J sao cho BHIJ là hình bình hành thì BJ ⊥ (P),