Chứng minh rằng Q là trung điểm của CM , N là trung điểm của CQ

Ôn tập chương I

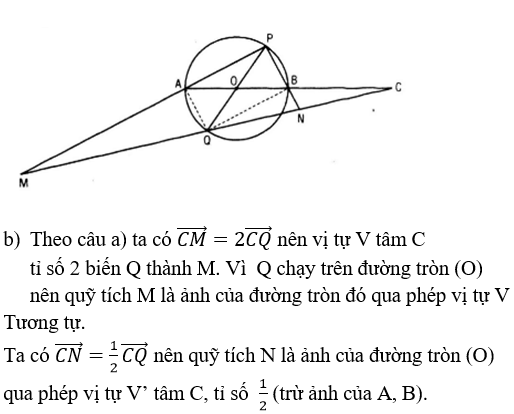
Bài 8 (trang 35 sgk Hình học 11 nâng cao): Cho đường tròn (O) có đường kính AB . Gọi C là điểm đối xứng với A qua B và PQ là đường kính thay đổi của (O) khác đường kính AB. Đường thẳng CQ cắt PA và PB lần lượt tại M và N.

a) Chứng minh rằng Q là trung điểm của CM , N là trung điểm của CQ

b) Tìm quỹ tích các điểm M và N khi đường kính PQ thay đổi

Lời giải:

a) Ta có QB // AP (vì cùng vuông góc với PB) và B là trung điểm của AC nên Q là trung điểm của CM

Ta có : AQ // BN (vì cùng vuông góc với AP) và B là trung điểm của AC nên N là trung điểm của PQ.