Viết phương trình mặt phẳng trong mỗi trường hợp sau: Đi qua ba điểm M(2, 0, -1)

Bài 2: Phương trình mặt phẳng

Haylamdo biên soạn và sưu tầm lời giải Bài 15 trang 89 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 15 (trang 89 sgk Hình Học 12 nâng cao): Viết phương trình mặt phẳng trong mỗi trường hợp sau:

a) Đi qua ba điểm M(2, 0, -1), N(1, -2, 3), P(0, 1, 2).

b) Đi qua hai điểm A(1, 1, -1), B(5, 2, 1) và song song với trục Oz.

c) Đi qua điểm (3, 2, -1) và song song với mặt phẳng có phương trình: x – 5y + z=0

d) Đi qua hai điểm A(0; 1; 1), B(-1; 0; 2) và vuông góc với mặt phẳng x - y + z + 1 = 0

e) Đi qua điểm M(a, b, c) (abc ≠ 0) và song song với một mặt phẳng tọa đố.

f) Đi qua điểm G(1, 2, 3) và cắt các trục tọa độ tại các điểm A, B, C sao cho G là trọng tâm tam giác ABC

g) Đi qua điểm H(2, 1, 1) và cắt trục tọa độ tại các điểm A, B, C sao cho H là trung trực tâm tam giác ABC.

Lời giải:

a) Mặt phẳng (MNP) nhận vectơ [MN→,MP→ ] là vectơ pháp tuyến. Ta có MN→=(-1,-2,4),MP→=(-2,1,3) nên [ MN→,MP→ ]=(-10,-5,-5). Vậy mp(MNP) đi qua M(2, 0, -1) và vectơ pháp tuyến là (-10, -5, -5) nên ta có phương trình: -10(x-2)-5y-5(z+1)=0 <=> 2x + y + z – 3 = 0

b) Vì mặt phẳng đi qua AB và song song với Oz nên nó có vectơ pháp tuyến là n→=[AB→,k→], với AB→=(4,1,2),k→=(0,0,1) nên n→=(1,-4,0)

Vậy mặt phẳng cần tìm đi qua A(1, 1, -1) và có vectơ pháp tuyến là n→=(1,-4,0) nên ta có Phương trình là: 1(x-1)-4(y-1)+0(z+1)=0

<=> x – 4y + 3 = 0

Cách khác:

Vì mặt phẳng cần tìm song song với Oz nếu có phương trình dạng Ax + By + D = 0, với A² + B² ≠ 0

Vì mặt phẳng này đi qua A(1, 1, -1) và B(5, 2, 1) nên ta có:

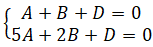
⇒ 4A + B = 0, nếu A = 0 thì B = 0 (loại)

Vậy A ≠ 0,ta chọn A = 1 ⇒ B = -4, và D = 3

Vậy phương trình mặt phẳng là: x – 4y + 3 = 0

c) Vì mặt phẳng cần tìm song song với mp: x – 5y + z = 0, nên nó có phương trình dạng: x – 5y + z + D = 0, mà mặt phẳng này lại đi qua điểm (3, 2, -1) nên ta có:

3 - 5.2 + (-1) + D = 0 ⇔ D = 8

Vậy phương trình mặt phẳng cần tìm là : x - 5y + z + 8 = 0

d) Vì mặt phẳng cần tìm đi qua AB và vuông góc với mặt phẳng: x – y + z + 1 = 0 nên có vectơ pháp tuyến là n→=[AB→,n₁→], với AB→=(-1,-1,1) và n₁→=(1,-1,1) là vectơ pháp tuyến của mặt phẳng: x-y+z+1=0. Suy ra n→=(0,2,2).

Vậy phương trình mặt phẳng cần tìm là: 0(x- 0)+2(y-1)+2( z- 1)= 0 hay y + z – 2 = 0

e) * Nếu mặt phẳng cần tìm song song với mp(Oxy) thì nó có vectơ pháp tuyến là n→=(0,0,1), mặt khác mặt phẳng này đi qua điểm M(a, b, c) nên có phương tình là: z – c = 0.

Tương tự, nếu mặt phẳng cần tìm đi qua M(a, b, c) và song song với mp(Oxz) thì có Phương trình: y – b = 0.

* Nếu mặt phẳng đó đi qua M(a, b, c) và song song với mp(Oyz) thì có phương trình: z - c = 0

f) Giả sử 3 giao điểm A, B, C của mặt phẳng với 3 trục tọa độ là A(a, 0, 0), B(0, b, 0), C(0, 0, c). vì G(1, 2, 3) là trọng tâm của ΔABC nên ta có:

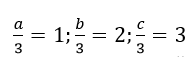
suy ra a = 3, b= 6, c = 9 nên ta có Phương trình mp(ABC) theo đoạn chắn là :

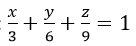
g) Giả sử 3 giao điểm A, B, C của mặt phẳng với 3 trục tọa độ là: A(a, 0, 0); B(0, b, 0); C(0, 0, c).

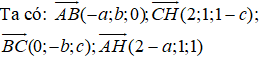
Vì H(2, 1, 1) là trực tâm ΔABC nên.

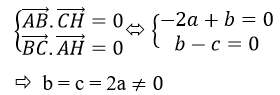
Khi đó, phương trình mặt phẳng (ABC) viết theo đoạn chắn là:

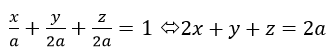
Mặt khác, mặt phẳng này đi qua H(2, 1, 1) nên ta có:

2.2 + 1 + 1 = 2a <=> a = 3

Vậy phương trình mặt phẳng cần tìm là: 2x+y+z-6=0