Cho hai mặt phẳng có phương trình lần lượt là: 2x-my+3z-6+m=0 và (m+3)x-2y+(5m+1)z-10=0

Bài 2: Phương trình mặt phẳng

Haylamdo biên soạn và sưu tầm lời giải Bài 18 trang 90 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 18 (trang 90 sgk Hình Học 12 nâng cao): Cho hai mặt phẳng có phương trình lần lượt là:

2x-my+3z-6+m=0 và (m+3)x-2y+(5m+1)z-10=0

Với giá trị nào của m thì:

a) Hai mặt phẳng song song.

b) Hai mặt phẳng trùng nhau.

c) Hai mặt phẳng đó cắt nhau.

d) Hai mặt phẳng vuông góc.

Lời giải:

Các hệ số của phương trình mặt phẳng: 2x-my+3z-6+m=0 là: A = 2, B = -m, C = 3, D = m – 6

Các hệ số của phương trình mặt phẳng là: (m+3)x-2y+(5m+1)z-10=0: A’ = m + 3; B’ = -2, C’ = 5m + 1; d’ = -10

a) Để hai mặt phẳng đã cho song song với nhau là:

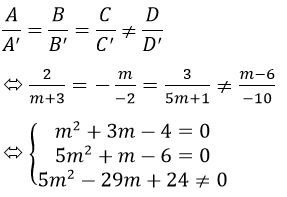
Hệ này vô nghiệm, nên không có m để hai mặt phẳng song song.

b) Để hai mặt phẳng đã cho trùng với nhau là:

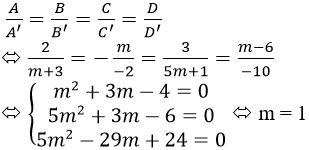
c) Hai mặt phẳng cắt nhau khi và chỉ khi chúng không trùng nhau (vì theo câu a, hai mặt này không thể song song với nhau). Theo câu b) ta suy ra giá trị m đẻ hai mặt phẳng cắt nhau là: m ≠ 1

d) Hai vectơ pháp tuyến của hai mặt phẳng lần lượt là: n₁→(2,-m,3) và n₂→(m+3),-2,5m+1)

Để hai mặt phẳng vuông góc thì n₁→⊥n₂→ hay n₁→.n₂→=0

<=> 2(m+3)+2m+3(5m+1)=0 <=> m=-9/19.

Vậy m =-9/19 là giá trị cần tìm.