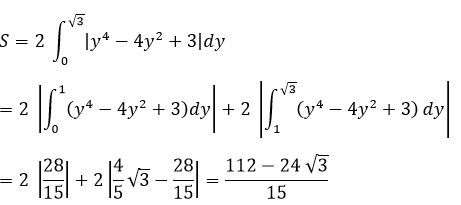Tính diện tích hình phẳng giới hạn bởi: Đồ thị các hàm số y=4-x^2; y=-x+2
Câu hỏi và bài tập ôn tập chương 3
Haylamdo biên soạn và sưu tầm lời giải Bài 51 trang 176 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.
Bài 51 (trang 176 sgk Giải Tích 12 nâng cao): Tính diện tích hình phẳng giới hạn bởi
a) Đồ thị các hàm số y=4-x2;y=-x+2
b) Các đường cong có Phương trình x=4-4y2 và x=1-y4
Lời giải:
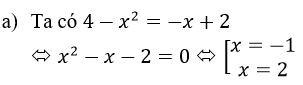
Vậy diện tích hình phẳng cần tìm là:
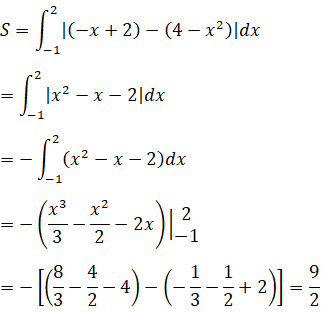
b) Tung độ giao điểm của hai đường cong là nghiệm của Phương trình
4-4y2=1-y4 <=> y4-4y4+3=0
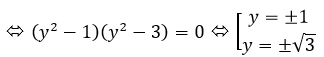
Xét dấu (y2-1)(y2-3) ta có
| y | -∞ | -√3 | -1 | 1 | √3 | +∞ | |||||
| y2 - 1 | + | | | + | 0 | - | 0 | + | | | + | ||
| y2 - 3 | + | 0 | - | | | - | | | - | 0 | + | ||
| (y2 - 1)(y2 - 3) | + | 0 | - | 0 | + | 0 | - | 0 | + |
Diện tích hình phẳng cần tìm là:
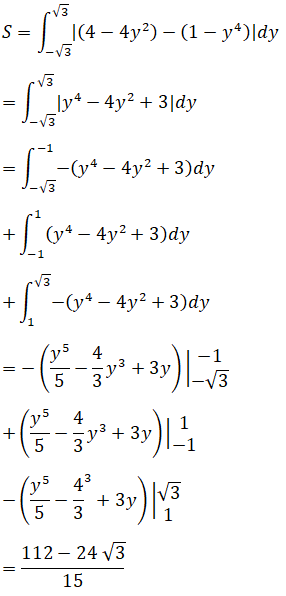
Chú ý. Ta có thể làm theo cách khác như sau mà không cần lập bảng xét dấu:
Vì hai đường đã cho cắt nhau tại 4 điểm có tung độ lần lượt là -√3; -1;1;√3 nên mỗi khoảng (-√3; -1);(-1;1);(1;√3) thì biểu thức y4-4y2+3 giữ nguyên một dấu vậy
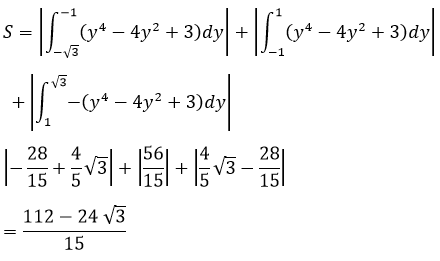
Ta cũng có thể dựa vào tính đối xứng qua Ox của cả hai đường cong để tính gọn hơn