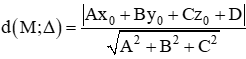Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C 0; 0; 1

Toán lớp 12 Ôn tập chương 3 Hình học 12

Bài 1 (trang 91 SGK Hình học 12): Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1), D(-2; 1; -1)

a) Chứng minh A, B, C, D là bốn đỉnh của một tứ diện.

b) Tìm góc giữa hai đường thẳng AB và CD

c) Tính độ dại đường cao của hình chóp A.BCD

Lời giải:

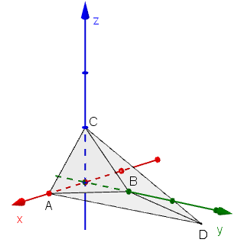
a) Cách 1:

Phương trình đoạn chắn (ABC) là:

hay x + y + z – 1 = 0.

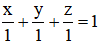
Thay tọa độ điểm D(-2; 1; -1) ta được: (-2) + 1 + (-1) – 1 = -3 ≠ 0

⇒ D không nằm trong (ABC)

⇒ A, B, C, D không đồng phẳng

⇒ A, B, C, D là bốn đỉnh của một tứ diện.

Cách 2:

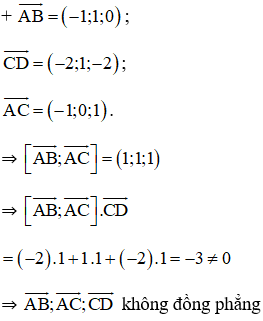
⇒ A, B, C, D không đồng phẳng

⇒ A, B, C, D là bốn đỉnh của hình tứ diện.

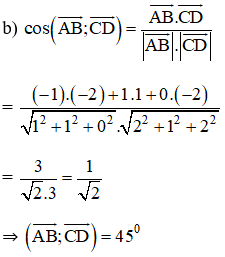
c) Độ dài đường cao hình chóp A.BCD chính là khoảng cách từ A đến (BCD).

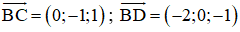
⇒ (BCD) nhận 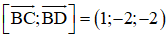là 1 vtpt

⇒ (BCD): x – 2y – 2z + 2 = 0

⇒ Độ dài đường cao hình chóp A.BCD là:

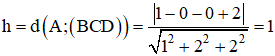
Kiến thức áp dụng

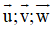
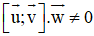
+ Ba vectơ không đồng phẳng nếu

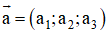
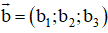
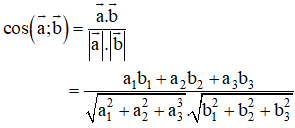
+ Góc giữa hai vec tơ và là :

+ Khoảng cách từ M(x₀ ; y₀ ; z₀) đến mặt phẳng (Δ): Ax + By + Cz + D = 0 là: