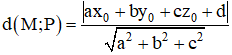Cho bốn điểm A(-2; 6; 3), B(1; 0; 6), C 0; 2; -1

Toán lớp 12 Ôn tập chương 3 Hình học 12

Bài 3 (trang 92 SGK Hình học 12): Cho bốn điểm A(-2; 6; 3), B(1; 0; 6), C(0; 2; -1), D(1; 4; 0)

a) Viết phương trình mặt phẳng (BCD). Suy ra ABCD là một tứ diện.

b) Tính chiều cao AH của tứ diện ABCD.

c) Viết phương trình mặt phẳng (α) chứa AB và song song với CD.

Lời giải:

a)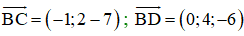

(BCD) nhận 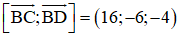là 1 vtpt

⇒ (BCD): 16x – 6y – 4z + 8 = 0

hay (BCD): 8x – 3y – 2z + 4 = 0.

b) Chiều cao AH của tứ diện ABCD chính là khoảng cách từ điểm A đến mp (BCD) :

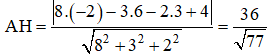
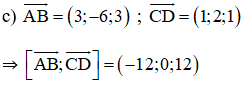
(α) chứa AB và song song với CD

⇒ (α) nhận (1; 0; -1) là 1 vtpt

(α) đi qua A(-2; 6; 3)

⇒ (α): x – z + 5 = 0.

Kiến thức áp dụng

+ A, B, C, D là bốn đỉnh của một tứ diện nếu chúng không đồng phẳng.

+ Khoảng cách từ điểm M(x₀ ; y₀ ; z₀) đến mặt phẳng (P) : ax + by + cz + d = 0 là :