Cho mặt cầu (S) có đường kính là AB biết rằng A 6; 2; -5
Toán lớp 12 Ôn tập chương 3 Hình học 12
Bài 2 (trang 91 SGK Hình học 12): Cho mặt cầu (S) có đường kính là AB biết rằng A(6; 2; -5), B(-4; 0; 7)
a) Tìm tọa độ tâm I và bán kính r của mặt cầu (S).
b) Lập phương trình của mặt cầu (S).
c) Lập phương trình của mặt phẳng (α) tiếp xúc với mặt cầu (S) tại điểm A
Lời giải:
a) Tâm của mặt cầu (S) là trung điểm I (1; 1; 1) của đoạn thẳng AB và bán kính của mặt cầu (S) là R = IA = √62
b) Mặt cầu (S) có phương trình là
(x - 1)2 + (y - 1)2 + (z - 1)2 = 62
c) (α) tiếp xúc với (S) tại A
⇒ (α) ⊥ IA
⇒ (α) nhận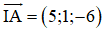 
là vectơ pháp tuyến
(α) đi qua A(6; 2; -5)
⇒ (α): 5x + y – 6z – 62 = 0.
Kiến thức áp dụng
+ Phương trình mặt cầu tâm I(a ; b ; c), bán kính R là:
(x – a)2 + (y – b)2 + (z – c)2 = R2.
+ Phương trình mặt phẳng (P) đi qua M(x0; y0; z0) và nhận n→ = (a; b; c) là vtpt là: a.(x – x0) + b(y – y0) + c(z – z0) = 0.
