Khảo sát tự biến thiên và vẽ đồ thị của các hàm số bậc bốn sau

---

Toán lớp 12 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Bài 2 (trang 43 SGK Giải tích 12): Khảo sát tự biến thiên và vẽ đồ thị của các hàm số bậc bốn sau:

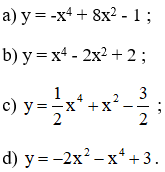
Lời giải:

a) Hàm số y = -x⁴ + 8x² – 1.

1) Tập xác định: D = R

2) Sự biến thiên:

+ Chiều biến thiên:

y' = -4x³ + 16x = -4x(x² - 4)

y' = 0 ⇔ -4x(x² - 4) = 0 ⇔ x = 0 ; x = ±2

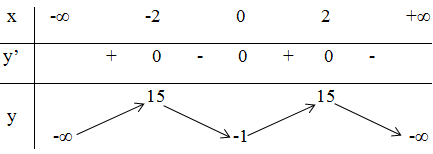
Trên khoảng (-∞; -2) và (0; 2), y’ > 0 nên hàm số đồng biến.

Trên các khoảng (-2; 0) và (2; +∞), y’ < 0 nên hàm số nghịch biến.

+ Cực trị :

Hàm số đạt cực đại tại x = 2 và x = -2 ; yCĐ = 15

Hàm số đạt cực tiểu tại x = 0 ; yCT = -1.

+ Giới hạn:

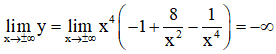
+ Bảng biến thiên:

3) Đồ thị:

+ Hàm số đã cho là hàm số chẵn, vì:

y(-x) = -(-x)⁴ + 8(-x)² - 1 = -x⁴ + 8x² - 1 = y(x)

⇒ Đồ thị nhận Oy làm trục đối xứng.

+ Giao với Oy tại điểm (0; -1) (vì y(0) = -1).

+ Đồ thị hàm số đi qua (-3; -10) và (3; 10).

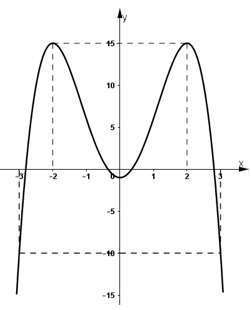
b) Hàm số y = x⁴ – 2x² + 2.

1) Tập xác định: D = R

2) Sự biến thiên:

+ Chiều biến thiên:

y' = 4x³ - 4x = 4x(x² - 1)

y' = 0 ⇔ 4x(x² - 1) = 0 ⇔ x = 0 ; x = ±1.

+ Giới hạn:

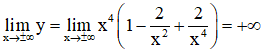
+ Bảng biến thiên:

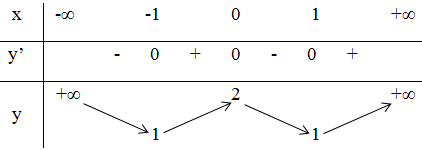
Kết luận :

Hàm số đồng biến trên khoảng (-1; 0) và (1; +∞).

Hàm số nghịch biến trên các khoảng (-∞; -1) và (0; 1).

Đồ thị hàm số có hai điểm cực tiểu là: (-1; 1) và (1; 1).

Đồ thị hàm số có điểm cực đại là: (0; 2)

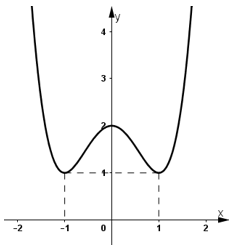
3) Đồ thị:

+ Hàm số chẵn nên đồ thị hàm số nhận trục Oy là trục đối xứng.

+ Đồ thị hàm số cắt trục tung tại (0; 2).

+ Đồ thị hàm số đi qua (-1; 1) và (1; 1).

+ Đồ thị hàm số:

c) Hàm số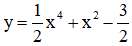

1) Tập xác định: D = R

2) Sự biến thiên:

+ y' = 2x³ + 2x = 2x(x² + 1)

   y' = 0 ⇔ 2x(x² + 1) = 0 ⇔ x = 0

+ Giới hạn:

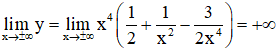
+ Bảng biến thiên:

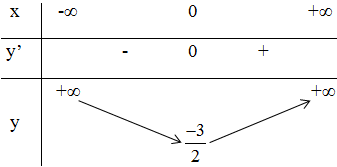
Kết luận: Hàm số đồng biến trên khoảng (0; +∞).

Hàm số nghịch biến trên các khoảng (-∞; 0).

Đồ thị hàm số có điểm cực đại là: (0; -3/2).

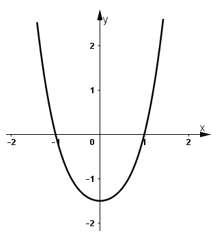
3) Đồ thị:

+ Hàm số chẵn nên nhận trục Oy là trục đối xứng.

+ Hàm số cắt trục hoành tại điểm (-1; 0) và (1; 0).

+ Hàm số cắt trục tung tại điểm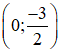

d) Hàm số y = -2x² – x⁴ + 3.

1) Tập xác định: D = R

2) Sự biến thiên:

+ Chiều biến thiên:

y' = -4x - 4x³ = -4x(1 + x²)

y' = 0 ⇔ -4x(1 + x²) = 0 ⇔ x = 0

+ Giới hạn:

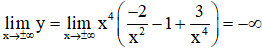
+ Bảng biến thiên:

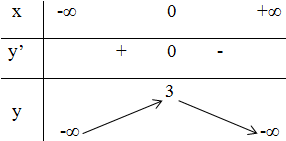
Kết luận: Hàm số đồng biến trên khoảng (-∞; 0).

Hàm số nghịch biến trên các khoảng (0; +∞).

Đồ thị hàm số có điểm cực đại là: (0; 3).

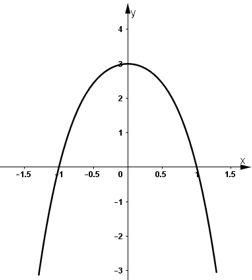
3) Đồ thị:

+ Hàm số là hàm số chẵn nên nhận trục Oy là trục đối xứng.

+ Hàm số cắt trục Ox tại (-1; 0) và (1; 0).

+ Hàm số cắt trục Oy tại (0; 3).

Kiến thức áp dụng