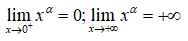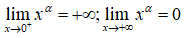Khảo sát sự biến thiên và vẽ đồ thị của các hàm số
Toán lớp 12 Bài 2: Hàm số lũy thừa
Bài 3 (trang 61 SGK Giải tích 12): Khảo sát sự biến thiên và vẽ đồ thị của các hàm số:
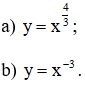
Lời giải:
a) Xét hàm số 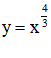
- Tập khảo sát : (0 ; +∞).
- Sự biến thiên:
+ 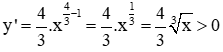
Do đó, hàm số đã cho đồng biến trên tập xác định.
+ Giới hạn:
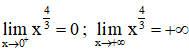
+ Tiệm cận : Đồ thị hàm số không có tiệm cận.
+ Bảng biến thiên:
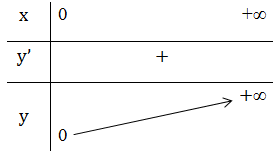
- Đồ thị hàm số:
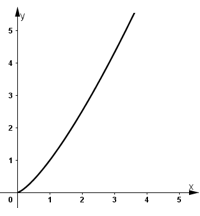
b) Xét hàm số y = x-3, ta có :
- Tập khảo sát : (0 ; +∞).
- Sự biến thiên:
+ y' = -3.x-3 - 1 = -3.x-4 < 0 với ∀ x > 0.
Do đó, hàm số đã cho nghịch biến trên tập xác định.
+ Giới hạn:
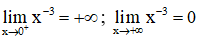
⇒ x = 0 (trục Oy) là tiệm cận đứng của đồ thị hàm số
y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.
+ Bảng biến thiên:
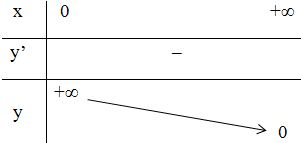
- Đồ thị:
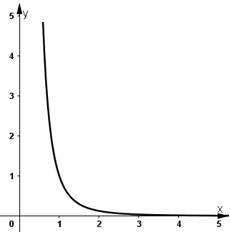
Kiến thức áp dụng
| y = xα; α > 0 | y = xα; α < 0 |
|
1. Tập khảo sát: (0; +∞) 2. Sự biến thiên y' = α.xα - 1 > 0; ∀x > 0 Giới hạn đặc biệt
Tiệm cận: Không có + Đồ thị hàm số luôn đi qua điểm (1;1) |
1. Tập khảo sát: (0; +∞) 2. Sự biến thiên y' = α.xα - 1 < 0; ∀x > 0 Giới hạn đặc biệt
Tiệm cận: Trục Ox là tiệm cận ngang Trục Oy là tiệm cận đứng + Đồ thị hàm số luôn đi qua điểm (1; 1) |