Cho hàm số y = 2x2 + 2mx + m - 1 có đồ thị là Cm

Toán lớp 12 Bài ôn tập chương I

Bài 5 (trang 45 SGK Giải tích 12): Cho hàm số y = 2x² + 2mx + m - 1 có đồ thị là (C_m), m là tham số.

a) Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m = -1

b) Xác định m để hàm số:

    i) Đồng biến trên khoảng (-1; +∞)

    ii) Có cực trị trên khoảng (-1; +∞)

c) Chứng minh rằng (C_m) luôn cắt trục hoành tại hai điểm phân biệt với mọi m.

Lời giải:

a) Với m = 1 ta được hàm số: y = 2x² + 2x

- TXĐ: D = R,

- Sự biến thiên:

+ Chiều biến thiên: y' = 4x + 2

y' = 0 ⇔ x = -1/2

+ Bảng biến thiên:

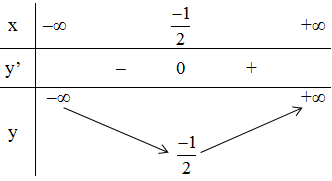
Kết luận: Hàm số nghịch biến trên (-∞; -1/2), đồng biến trên (-1/2; +∞).

Đồ thị hàm số có điểm cực tiểu là (-1/2; -1/2)

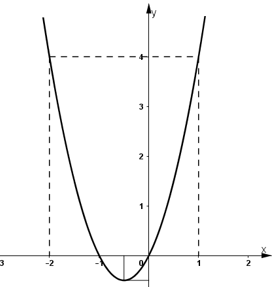
- Đồ thị:

Ta có: 2x² + 2x = 0 ⇔ 2x(x + 1) = 0

⇒ x = 0; x = -1

+ Giao với Ox: (0; 0); (-1; 0)

+ Giao với Oy: (0; 0)

b) Xét hàm số y = 2x² + 2mx + m - 1

y' = 4x + 2m = 2(2x + m)

y' = 0 ⇒ x = -m/2

Ta có bảng xét biến thiên :

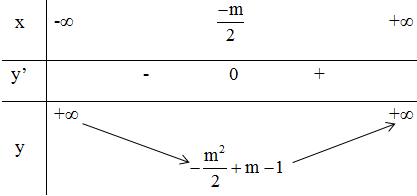
Từ bảng biến thiên ta thấy :

- Hàm số đồng biến trên khoảng (-1; +∞)

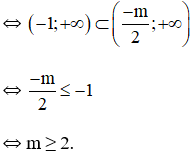
- Hàm số có cực trị trên khoảng (-1; +∞)

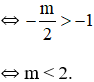
c) Nhận thấy: 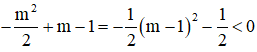với mọi m.

Suy ra, giá trị cực tiểu luôn nhỏ hơn 0 với mọi m.

Dựa vào bảng biến thiên suy ra đường thẳng y = 0 (trục hoành) luôn cắt đồ thị hàm số tại 2 điểm phân biệt (đpcm).