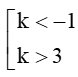Tìm k sao cho phương trình x^2 + y^2 – 6x + 2ky + 2k + 12 = 0

Tìm k sao cho phương trình: x + y – 6x + 2ky + 2k + 12 = 0 là phương trình đường tròn.

Giải sách bài tập Toán 10 Bài 5: Phương trình đường tròn

Bài 53 trang 89 SBT Toán 10 Tập 2: Tìm k sao cho phương trình: x² + y² – 6x + 2ky + 2k + 12 = 0 là phương trình đường tròn.

Lời giải:

Ta biến đổi như sau:

x² + y² – 6x + 2ky + 2k + 12 = 0

⇔ (x – 3)² + (y + k)² = k² – 2k – 3

Để phương trình trên là phương trình đường tròn thì

k² – 2k – 3>0$\iff$

Vậy k < – 1 hoặc k > 3.