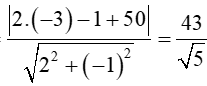Trong mặt phẳng tọa độ Oxy, cho các đường thẳng ∆1 x+y+1=0; ∆2 3x+4y+20=0

Trong mặt phẳng tọa độ Oxy, cho các đường thẳng: : x+y+1=0, : 3x+4y+20=0; : 2x-y+50=0 và đường tròn (C); (x+3)+(y-1)=9 . Xác định vị trí tương đối của các đường thẳng đã cho đối với đường tròn (C).

Giải sách bài tập Toán 10 Bài 5: Phương trình đường tròn

Bài 57 trang 90 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho các đường thẳng: ${\Delta }_1$: x+y+1=0, ${∆}_2$: 3x+4y+20=0; ${∆}_3$: 2x-y+50=0 và đường tròn (C); (x+3)²+(y-1)²=9 . Xác định vị trí tương đối của các đường thẳng đã cho đối với đường tròn (C).

Lời giải:

Đường tròn (C) có tâm I(-3; 1) và bán kính R = 3.

Ta có: d(I,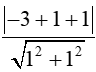${\Delta }_1$)=<3, suy ra ${\Delta }_1$ cắt đường tròn tại hai điểm phân biệt.

d(I,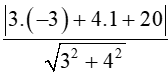${∆}_2$)==$\frac{15}{5}$=3=R, suy ra ${∆}_2$ tiếp xúc với đường tròn.

d(I,${∆}_3$)=>3, suy ra ${∆}_3$ không có điểm chung với đường tròn.