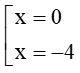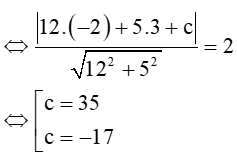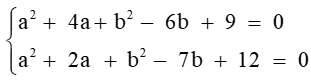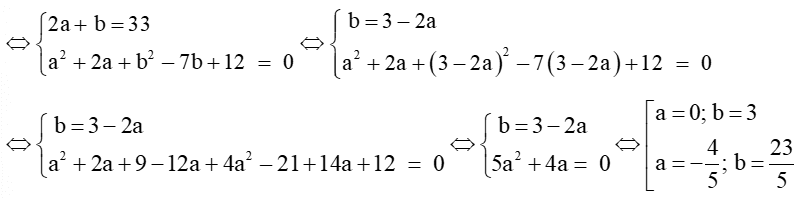Lập phương trình đường thẳng ∆ là tiếp tuyến của đường tròn (C) (x+2)^2+(y-3)^2=4

Lập phương trình đường thẳng ∆ là tiếp tuyến của đường tròn (C): (x+2)+(y-3)=4 trong mỗi trường hợp sau:

Giải sách bài tập Toán 10 Bài 5: Phương trình đường tròn

Bài 55 trang 89 SBT Toán 10 Tập 2: Lập phương trình đường thẳng ∆ là tiếp tuyến của đường tròn (C): (x+2)²+(y-3)²=4 trong mỗi trường hợp sau:

a) ∆ tiếp xúc (C) tại điểm có tung độ bằng 3.

b) ∆ vuông góc với đường thẳng 5x – 12y + 1 = 0.

c) ∆ đi qua điểm D(0; 4).

Lời giải:

Đường tròn có tâm I(-2; 3) và bán kính R = 2.

a) Hoành độ của điểm có tung độ bằng 3 là:

(x+2)²+(3-3)²=4 $\iff$

Suy ra ta có 2 điểm M(0; 3) và điểm N(-4; 3).

Vectơ pháp tuyến của đường thẳng IM là: $\overrightarrow{IM}$=(2;0).

Phương trình đường thẳng IM: 2(x – 0) = 0 hay x = 0.

Vectơ pháp tuyến của đường thẳng IN là: $\overrightarrow{IN}$=(-2;0).

Phương trình đường thẳng IN: - 2(x + 4) = 0 hay x + 4 = 0.

Vậy phương trình đường thẳng là: x = 0 hoặc x + 4 = 0.

b) ∆ vuông góc với đường thẳng 5x – 12y + 1 = 0

nên ∆ có dạng: 12x + 5y + c = 0.

Khoảng cách từ I đến ∆ bằng R nên d(I,∆)=2

Với c = 35 thì phương trình tiếp tuyến là: 12x + 5y + 35 =0

Với c = - 17 thì phương trình tiếp tuyến là: 12x + 5y – 17 =0

c) Gọi H(a ;b) là tiếp điểm.

Do D(0; 4) thuộc nên DH vuông góc với IH và IH = R = 2.

Ta có: $\overrightarrow{DH}$=(a;b-4) và $\overrightarrow{IH}$=(a+2;b-3)

⇒ IH = |$\overrightarrow{IH}$|=$\sqrt{{\left(a+2\right)}^2+{\left(b-3\right)}^2}$=2

⇔ a² + 4a + 4 + b² – 6b + 9 = 4

⇔ a² + 4a + b² – 6b + 9 = 0 (1)

Ta lại có: $\overrightarrow{DH}$.$\overrightarrow{IH}$=0$\iff$ a(a+2)+(b-4)(b-3)=0

⇔ a² + 2a + b² – 7b + 12 = 0 (2)

Từ (1) và (2) ta có hệ phương trình:

Với a = 0, b = 3 thì H(0; 3)

Suy ra $\overrightarrow{IH}$=(2;0)

Do đó phương trình tiếp tuyến cần tìm là: 2(x – 0) = 0 ⇔ x = 0.

Với a=$-\frac{4}{5}$; b=$\frac{23}{5}$

Suy ra $\overrightarrow{IH}$= $\left(\frac{6}{5};\frac{8}{5}\right)=\frac{2}{5}\left(3;4\right)$

Do đó phương trình tiếp tuyến cần tìm là: 3(x – 0) + 4(y – 4) = 0 ⇔ 3x + 4y – 16 = 0.

Vậy có hai đường thẳng ∆ thỏa mãn yêu cầu là x = 0 hoặc 3x + 4y – 16 = 0.