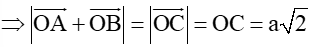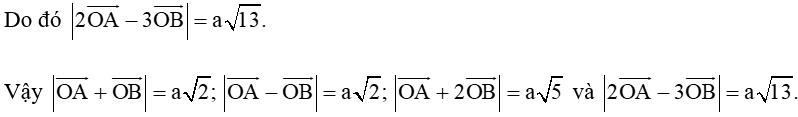Cho tam giác OAB vuông cân, với OA = OB = a

Sách bài tập Toán 10 Kết nối tri thức Bài 9: Tích của một vectơ với một số

Bài 4.14 trang 54 sách bài tập Toán lớp 10 Tập 1:

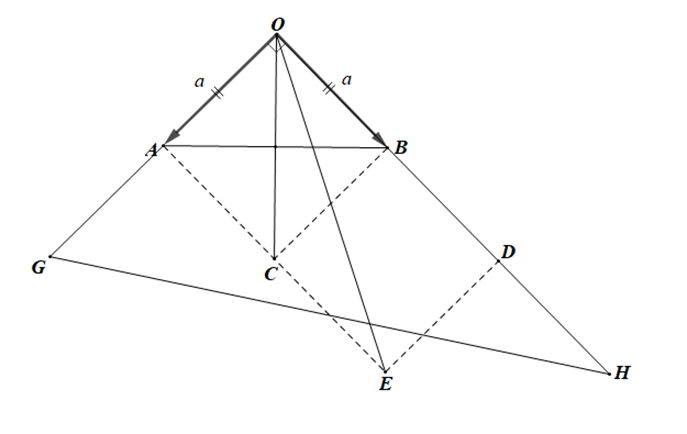
Cho tam giác OAB vuông cân, với OA = OB = a. Hãy xác định độ dài của các vectơ sau $\overrightarrow{OA}-\overrightarrow{OB},$ $\overrightarrow{OA}-\overrightarrow{OB},$ $\overrightarrow{OA}+2\overrightarrow{OB},$ $2\overrightarrow{OA}-3\overrightarrow{OB}.$

Lời giải:

Gọi C là điểm thoả mãn OACB là hình bình hành

Mà ∆OAB vuông cân có OA = OB nên OACB là hình vuông

$\Rightarrow$ OC = AB

Mà AB² = OA² + OB² (định lí Pythagoras)

$\Rightarrow$ AB² = a² + a² = 2a²

$\Rightarrow OC=AB=a\sqrt{2}$

+) Có: $\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OC}$ (quy tắc hình bình hành)

+) Có: $\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{BO}=\overrightarrow{BO}+\overrightarrow{OA}=\overrightarrow{BA}$

+) Lấy điểm D sao cho $\overrightarrow{OD}=2\overrightarrow{OB}$ nên hai vectơ $\overrightarrow{OD}$, $\overrightarrow{OB}$ cùng hướng và OD = 2OB.

Có: $\overrightarrow{OA}+2\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{OD}$

Vẽ hình chữ nhật OAED, khi đó $\overrightarrow{OA}+\overrightarrow{OD}=\overrightarrow{OE}$

Mà OE² = OD² + DE² (định lí Pythagoras)

$\Rightarrow$ OE² = (2OB)² + OA²

$\Rightarrow$ OE² = (2a)² + a² = 5a²

$\Rightarrow OE=a\sqrt{5}$

+) Lấy điểm G sao cho $\overrightarrow{OG}=2\overrightarrow{OA},\overrightarrow{OH}=3\overrightarrow{OB}$

Khi đó: hai vectơ $\overrightarrow{OG}$, $\overrightarrow{OA}$ cùng hướng và OG = 2OA;

Và hai vectơ $\overrightarrow{OH}$, $\overrightarrow{OB}$ cùng hướng và OH = 3OB.

Có: $2\overrightarrow{OA}-3\overrightarrow{OB}=\overrightarrow{OG}-\overrightarrow{OH}$

$=\overrightarrow{OG}+\overrightarrow{HO}$$=\overrightarrow{HO}+\overrightarrow{OG}$

$=\overrightarrow{HG}$

Mà HG² = OG² + OH² (định lí Pythagoras)

$\Rightarrow$ HG² = (2OA)² + (3OB)²

$\Rightarrow$ HG² = (2a)² + (3a)²

$\Rightarrow$ HG² = 13a²

^{$\Rightarrow HG=a\sqrt{13}$}