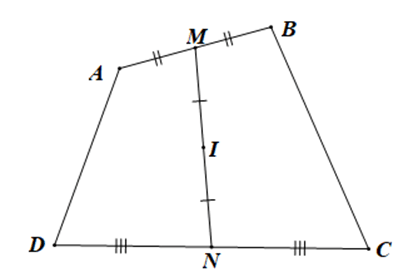
Cho tứ giác ABCD. Gọi M, N theo thứ tự là trung điểm các cạnh AB, CD

Cho tứ giác ABCD. Gọi M, N theo thứ tự là trung điểm các cạnh AB, CD và gọi I là trung điểm của MN. Chứng minh rằng với điểm O bất kì đều có

Sách bài tập Toán 10 Kết nối tri thức Bài 9: Tích của một vectơ với một số

Bài 4.16 trang 54 sách bài tập Toán lớp 10 Tập 1: Cho tứ giác ABCD. Gọi M, N theo thứ tự là trung điểm các cạnh AB, CD và gọi I là trung điểm của MN. Chứng minh rằng với điểm O bất kì đều có

$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=4\overrightarrow{OI}.$

Lời giải:

Với điểm O bất kì ta có:

+) $\overrightarrow{OA}+\overrightarrow{OB}=2\overrightarrow{OM}$ (do M là trung điểm của AB)

+) $\overrightarrow{OC}+\overrightarrow{OD}=2\overrightarrow{ON}$ (do N là trung điểm của CD)

+) $\overrightarrow{OM}+\overrightarrow{ON}=2\overrightarrow{OI}$ (do I là trung điểm của MN)

$\Rightarrow$$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=2\overrightarrow{OM}+2\overrightarrow{ON}$

$=2\left(\overrightarrow{OM}+\overrightarrow{ON}\right)=2.2\overrightarrow{OI}=4\overrightarrow{OI}$

Vậy với điểm O bất kì đều có: $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=4\overrightarrow{OI}.$