Bài 4.19 trang 54 sách bài tập Toán lớp 10 Tập 1
Sách bài tập Toán 10 Kết nối tri thức Bài 9: Tích của một vectơ với một số
Bài 4.19 trang 54 sách bài tập Toán lớp 10 Tập 1:
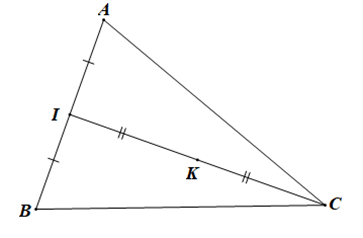
Cho tam giác ABC.
a) Tìm điểm M sao cho →MA+→MB+2→MC=→0.
b) Xác định điểm N thoả mãn 4→NA−2→NB+→NC=→0.
Lời giải:
a)
Gọi I là trung điểm của AB.
Khi đó: →MA+→MB=2→MI
⇒→MA+→MB+2→MC=2→MI+2→MC=2(→MI+→MC)
Gọi K là trung điểm của IC, khi đó: →MI+→MC=2→MK
⇒→MA+→MB+2→MC=2.2→MK=4→MK.
Mà →MA+→MB+2→MC=→0.
Do đó 4→MK=→0⇔→MK=→0
Suy ra M ≡ K.
Vậy M là trung điểm của IC (với I là trung điểm của AB).
b)
Ta có: 4→NA−2→NB+→NC=4→NA−2(→NA+→AB)+→NC
=4→NA−2→NA−2→AB+→NC
=2→NA−2→AB+→NC
=→NA−2→AB+(→NA+→NC)
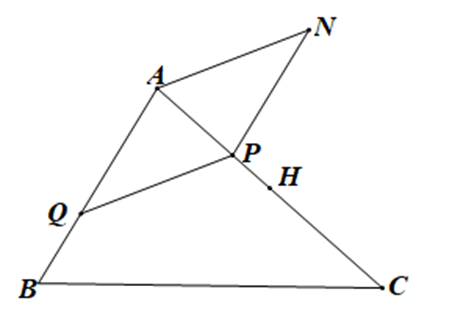
Gọi H là trung điểm của AC, khi đó →NA+→NC=2→NH
⇒4→NA−2→NB+→NC=→NA−2→AB+2.→NH
=(→NA+2.→NH)−2→AB
Giả sử P là điểm thỏa mãn →PA+2.→PH=→0
Khi đó →NA+2.→NH=(→NP+→PA)+2(→NP+→PH)
=3→NP+→PA+2→PH
=3→NP+→0
=3→NP
⇒4→NA−2→NB+→NC=3→NP−2→AB
Mà 4→NA−2→NB+→NC=→0.
Nên 3→NP−2→AB=→0
⇒3→NP=2→AB
⇒→NP=23→AB
Gọi Q là điểm nằm trên cạnh AB sao cho →AQ=23→AB
⇒→NP=→AQ
Do đó tứ giác AQPN là hình bình hành
Vậy điểm N cần tìm là đỉnh của hình bình hành AQPN (với Q thỏa mãn →AQ=23→AB và P thỏa mãn →PA+2.→PH=→0, H là trung điểm của AC).
