Viết phương trình chính tắc của parabol (P), biết rằng (P) có đường chuẩn là đường thẳng Δ

Viết phương trình chính tắc của parabol (P), biết rằng (P) có đường chuẩn là đường thẳng Δ: x + 4 = 0. Tìm toạ độ điểm M thuộc (P) sao cho khoảng cách từ M đến tiêu điểm của (P) bằng 5.

Sách bài tập Toán 10 Kết nối tri thức Bài 22: Ba đường conic

Bài 7.33 trang 46 Sách bài tập Toán lớp 10 Tập 2: Viết phương trình chính tắc của parabol (P), biết rằng (P) có đường chuẩn là đường thẳng Δ: x + 4 = 0. Tìm toạ độ điểm M thuộc (P) sao cho khoảng cách từ M đến tiêu điểm của (P) bằng 5.

Lời giải:

Phương trình chính tắc của (P) có dạng y² = 2px, trong đó p > 0.

Vì (P) có đường chuẩn là Δ: x + 4 = 0 ⇔ x = –4 ⇔ –p : 2 = –4 ⇔ p = 8

Vậy phương trình chính tắc của (P) là y² = 16x.

Gọi M (x₀; y₀).

Vì M thuộc (P) nên ta có:

d(M, Δ) = MF = 5 với F là tiêu điểm của (P) và F(4; 0).

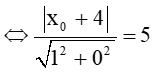
⇔ |x₀ + 4| = 5 (*)

TH1: x₀ + 4 ≥ 0 hay x₀ ≥ –4

(*) ⇔ x₀ + 4 = 5 ⇔ x₀ = 1 (thỏa mãn)

TH2: x₀ + 4 < 0 hay x₀ < –4

(*) ⇔ –x₀ – 4 = 5 ⇔ x₀ = –9 (thỏa mãn)

Với x₀ = –9, thay vào phương trình của (P) ta được y₀² = 16.(–9) = –144 < 0 (không thể tồn tại)

Với x₀ = 1, thay vào phương trình của (P) ta được y₀² = 16.1 = 16 ⇔ y₀ = ±4

Vậy M(1; 4) hoặc M(1; –4).