Cho điểm M(x0; y0) thuộc elip (E) có phương trình trang 29 SBT Toán lớp 10 Tập 2
Cho điểm M(x; y) thuộc elip (E) có phương trình .
Sách bài tập Toán 10 Kết nối tri thức Bài 22: Ba đường conic
Bài 7.36 trang 47 Sách bài tập Toán lớp 10 Tập 2: Cho điểm M(x0; y0) thuộc elip (E) có phương trình .
a) Tính MF12 – MF22 theo x0; y0. Từ đó tính MF1, MF2, theo x0; y0.
b) Tìm điểm M sao cho MF2 = 2MF1.
c) Tìm M sao cho góc nhìn của M tới hai đểm F1; F2 (tức là góc ) là lớn nhất ?
Lời giải:
Từ phương trình chính tắc của (E) ta có
b = 1, .
(E) có hai tiêu điểm là F1(–1; 0); F2(1; 0).
a)
Ta có:
MF12 = (x0 + 1)2 + (y0 – 0)2 = (x0 + 1)2 + y02
MF22 = (x0 – 1)2 + (y0 – 0)2 = (x0 – 1)2 + y02
MF12 – MF22
= (x0 + 1)2 + y02 – [(x0 – 1)2 + y02]
= (x0 + 1)2 – (x0 – 1)2
= x02 + 2x0 + 1 – (x02 – 2x0 + 1)
= 4x0.
Mặt khác, do M thuộc (E) nên ta có:
MF1 + MF2 = 2a = (1)
Mà: (MF1 – MF2)(MF1 + MF2) = MF12 – MF22
(2)
Cộng hai vế của (1) và (2) ta có:
2MF1 = +
⇔ MF1 = +
⇒ MF2 = .
b)
Sử dụng kết quả của phần a) ta có:
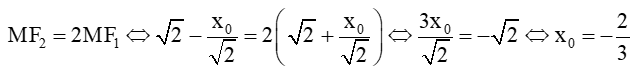
Mặt khác do M thuộc (E) nên ta có:
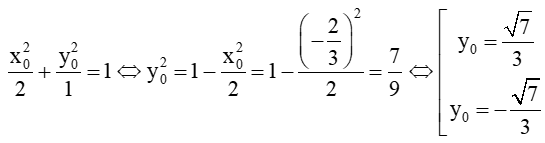
Vậy hoặc .
c)
Áp dụng định lí côsin trong tam giác MF1F2, ta có
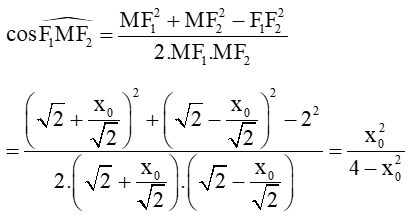
Ta có: ⇔ 0 ≤ x02 ≤ 2 ⇒ 4 – x02 > 0.
Suy ra
Dấu bằng xảy ra khi và chỉ khi x0 = 0 ⇒ y0 = ±1
Vậy M(0; 1) hoặc M(0; –1) thì M nhìn hai tiêu điểm dưới góc nhìn lớn nhất.

