Cho parabol (P) có phương trình là y^2 = 16x. Gọi Δ là đường thẳng bất kì

Cho parabol (P) có phương trình là y = 16x. Gọi Δ là đường thẳng bất kì đi qua tiêu điểm F của (P) và không trùng với trục hoành. Chứng minh rằng Δ luôn cắt (P) tại hai điểm phân biệt A, B, đồng thời tích các khoảng cách từ A và B đến trục hoành không đổi.

Sách bài tập Toán 10 Kết nối tri thức Bài 22: Ba đường conic

Bài 7.34 trang 46 Sách bài tập Toán lớp 10 Tập 2: Cho parabol (P) có phương trình là y² = 16x. Gọi Δ là đường thẳng bất kì đi qua tiêu điểm F của (P) và không trùng với trục hoành. Chứng minh rằng Δ luôn cắt (P) tại hai điểm phân biệt A, B, đồng thời tích các khoảng cách từ A và B đến trục hoành không đổi.

Lời giải:

Gọi vectơ chỉ phương của Δ là $\overrightarrow{u_{∆}}=\left(a;b\right)$. Vì Δ đi qua điểm F(4; 0) và Δ không trùng với trục Ox nên ta có b ≠ 0. Phương trình tham số của Δ là

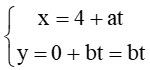
Toạ độ giao điểm của Δ và (P) ứng với thoả mãn phương trình

(bt)² =16 . (4 + at) ⇔ b²t² – 16at – 64 = 0. (1)

Phương trình (1) có Δ’ = 64a² + 64b² > 0 (do b ≠ 0), suy ra phương trình (1) luôn có 2 nghiệm phân biệt. Vậy Δ luôn cắt (P) tại hai điểm phân biệt A, B.

Gọi A(4 + at₁; bt₁), B(4 + at₂; bt₂), trong đó t₁, t₂ là hai nghiệm của phương trình (1).

Ta có

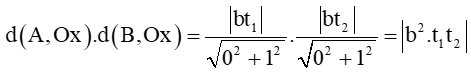
Dựa vào phương trình (1). Theo định lí Vi–ét ta có: $t_1{t}_2=\frac{-64}{b^2}$. Từ đó suy ra

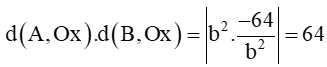
Vậy tích các khoảng cách từ A và B đến trục hoành không đổi.