Cho hình chóp S ABC có đáy ABC là tam giác đều canh a cạnh bên SA vuông góc với đáy

❮ Bài trước Bài sau ❯

Cho hình chóp S.ABC có đáy ABC là tam giác đều canh a, cạnh bên SA vuông góc với đáy. Tính khoảng cách từ điểm A đến mặt phẳng (SBC) theo a, biết SA = .

Giải sách bài tập Toán 11 Bài 4: Khoảng cách trong không gian - Chân trời sáng tạo

Bài 1 trang 68 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có đáy ABC là tam giác đều canh a, cạnh bên SA vuông góc với đáy. Tính khoảng cách từ điểm A đến mặt phẳng (SBC) theo a, biết SA = $\frac{a \sqrt{6}}{2}$ .

Lời giải:

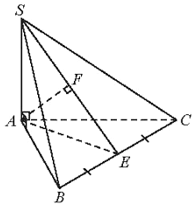
Cho hình chóp S ABC có đáy ABC là tam giác đều canh a cạnh bên SA vuông góc với đáy

Gọi E là trung điểm của BC thì BC ⊥ AE (vì ∆ABC đều).

Ta có BC ⊥ SA và BC ⊥ AE $\Rightarrow$ BC ⊥ (SAE).

$\Rightarrow$ (SBC) ⊥ (SAE).

Trong mặt phẳng (SAE), vẽ AF ⊥ SE (F $\in$ SE).

Suy ra AF ⊥ (SBC) hay d(A, (SBC))=AF.

Xét ∆SAE vuông tại A, ta có:

$\frac{1}{A F^{2}} = \frac{1}{A S^{2}} + \frac{1}{A E^{2}} = \frac{2}{3 a^{2}} + \frac{4}{3 a^{2}} = \frac{2}{a^{2}} \Rightarrow A F = \frac{a \sqrt{2}}{2}$ .

Vậy $d (S, (A B C)) = A F = \frac{a \sqrt{2}}{2}$ .

Lời giải SBT Toán 11 Bài 4: Khoảng cách trong không gian hay khác:

Xem thêm lời giải Sách bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯