Cho hàm số f(x) = x + căn (4-x^2). Tìm tập xác định của hàm số đã cho
Cho hàm số f(x) = x + .
Giải sách bài tập Toán 11 Bài tập cuối chương 9 - Kết nối tri thức
Bài 9.43 trang 65 SBT Toán 11 Tập 2: Cho hàm số f(x) = x + .
a) Tìm tập xác định của hàm số đã cho.
b) Tính đạo hàm f'(x) và tìm tập xác định của f'(x).
c) Tìm x sao cho f'(x) = 0.
Lời giải:
a) Điều kiện 4 – x2 0 −2 ≤ x ≤ 2.
Vậy tập xác định của hàm số là [−2; 2].
b) Có f'(x) = (x+)' = 1 +
.
Điều kiện để f'(x) xác định là 4 – x2 > 0 −2 < x < 2.
Vậy tập xác định của f'(x) là (−2; 2).
c) Có f'(x) = 0 thì
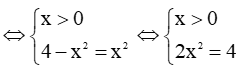
Kết hợp với điều kiện ở câu b, ta có là giá trị cần tìm.
Lời giải SBT Toán 11 Bài tập cuối chương 9 hay khác:
Bài 9.22 trang 63 SBT Toán 11 Tập 2: Cho f(x) = cos2. Đạo hàm f'(0) bằng ....
Bài 9.23 trang 63 SBT Toán 11 Tập 2: Cho f(x) = -x3+x2+3x - 1. Đạo hàm f'(x) > 0 khi ....
Bài 9.24 trang 63 SBT Toán 11 Tập 2: Đạo hàm của hàm số y = ln|1 – 2x| là ....
Bài 9.25 trang 63 SBT Toán 11 Tập 2: Đạo hàm của hàm số là ....
Bài 9.26 trang 63 SBT Toán 11 Tập 2: Đạo hàm của hàm số là ....
Bài 9.27 trang 63 SBT Toán 11 Tập 2: Đạo hàm của hàm số y = xsin2x là ....
Bài 9.28 trang 64 SBT Toán 11 Tập 2: Cho hàm số với g(0) = 3, g'(0) = −8. Đạo hàm f'(0) bằng ....
Bài 9.29 trang 64 SBT Toán 11 Tập 2: Cho f(x) = xsinx và g(x) = . Giá trị là ....
Bài 9.30 trang 64 SBT Toán 11 Tập 2: Cho f(x) = x. Tập nghiệm của phương trình f'(x) = 0 là ....

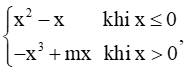 với m là tham số. Tìm m để hàm số có đạo hàm tại mọi x ℝ ....
với m là tham số. Tìm m để hàm số có đạo hàm tại mọi x ℝ ....