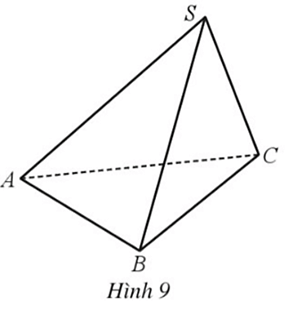
Cho hình chóp S.ABC có SA = SB = SC = AB = AC = a và BC = acăn2 (Hình 9)

Cho hình chóp S.ABC có SA = SB = SC = AB = AC = a và BC = (Hình 9).

Giải SBT Toán 12 Cánh diều Bài 1: Vectơ và các phép toán vectơ trong không gian

Bài 7 trang 61 SBT Toán 12 Tập 1: Cho hình chóp S.ABC có SA = SB = SC = AB = AC = a và BC = $\sqrt{2}$ (Hình 9).

a) Tam giác ABC vuông tại A và tam giác SAB đều.
b) $\vec{A B} . \vec{A C}$ = 0 và $(\vec{S A}, \vec{A B})$ = 120°.
c) $\vec{S C} . \vec{A B} = \frac{a^{2}}{2}$ .
d) $\cos (\vec{S C}, \vec{A B})$ = $\frac{1}{2}$ .

Lời giải:

a) Đ

b) Đ

c) S

d) S

Nhận thấy: AB² + AC² = a² + a² = 2a² = BC².

Định lý Pythagore đảo ta có tam giác ABC vuông tại A.

Có SA = SB = AB nên tam giác SAB đều.

Vì tam giác ABC vuông tại A nên $\vec{A B} . \vec{A C}$ = 0.

Ta có $(\vec{S A}, \vec{A B})$ = 180° − $\hat{S A B}$ = 120°.

Ta có: $\vec{S C} . \vec{A B} = (\vec{S A} + \vec{A C}) . \vec{A B}$ = $\vec{S A} . \vec{A B} + \vec{A C} . \vec{A B}$ = $\vec{S A} . \vec{A B}$

= | $\vec{S A}$ |.| $\vec{A B}$ |.cos120^o = $\frac{- a^{2}}{2}$ .

Suy ra $\cos (\vec{S C}, \vec{A B})$ = = $\frac{\frac{- a^{2}}{2}}{a^{2}}$ = $\frac{- 1}{2}$ .

Lời giải SBT Toán 12 Bài 1: Vectơ và các phép toán vectơ trong không gian hay khác: