Bác Hưng có một hàng rào thép dài 240 m và muốn rào cánh đồng thành một thửa ruộng
Bác Hưng có một hàng rào thép dài 240 m và muốn rào cánh đồng thành một thửa ruộng hình chữ nhật giáp một con sông thẳng. Bác không cần rào phía cạnh con sông. Hỏi thửa ruộng có diện tích lớn nhất là bao nhiêu?
Giải sách bài tập Toán 12 Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn - Kết nối tri thức
Bài 1.41 trang 31 SBT Toán 12 Tập 1: Bác Hưng có một hàng rào thép dài 240 m và muốn rào cánh đồng thành một thửa ruộng hình chữ nhật giáp một con sông thẳng. Bác không cần rào phía cạnh con sông. Hỏi thửa ruộng có diện tích lớn nhất là bao nhiêu?
Lời giải:
Gọi x, y (m) lần lượt là chiều dài hai cạnh của thửa ruộng hình chữ nhật. Giả sự cạnh giáp sông của thửa ruộng có độ dài là y (m).
Khi đó, theo đề bài ta có: 2x + y = 240 hay y = 240 – 2x.
Do đó: 0 < x < 120; y > 0.
Diện tích cửa thửa ruộng là
S = xy = x(240 – 2x) = 240x – 2x2, 0 < x < 120.
Ta có: S' = 240 – 4x
S' = 0 ⇔ x = 60 (vì 0 < x < 120).
Khi đó y = 240 – 2.60 = 120.
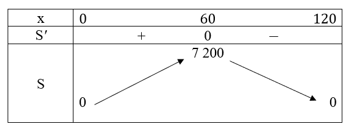
Lập bảng biến thiên:
Vậy thửa ruộng có diện tích lớn nhất là:
S = 60. 120 = 7 200 (m2) (khi cạnh giáp sông và cạnh đối diện có độ dài 120 m, hai cạnh kia có độ dài 60 m).
Chú ý: Nếu phải rào cả bốn cạnh cửa thửa ruộng thì dễ thấy thửa ruộng có diện tích lớn nhất khi nó là hình vuông, tức là bốn cạnh đều dài 60 m, và khi đó diện tích lớn nhất là 3 600 m2.
Lời giải Sách bài tập Toán lớp 12 Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn hay khác: