Một công ty ước tính rằng chi phí C (USD) để sản xuất x đơn vị sản phẩm

Một công ty ước tính rằng chi phí C (USD) để sản xuất x đơn vị sản phẩm có thể được mô hình hóa bằng công thức

Giải sách bài tập Toán 12 Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn - Kết nối tri thức

Bài 1.48 trang 32 SBT Toán 12 Tập 1: Một công ty ước tính rằng chi phí C (USD) để sản xuất x đơn vị sản phẩm có thể được mô hình hóa bằng công thức

C = 800 + 0,04x + 0,0002x².

Tìm mức sản xuất sao cho chi phí trung bình $\overline{C}\left(x\right)=\frac{C\left(x\right)}{x}$ cho mỗi đơn vị hàng hóa là nhỏ nhất.

Lời giải:

Ta có: $\overline{C}\left(x\right)=\frac{C\left(x\right)}{x}=\frac{800}{x}+0,04+0,0002x$

Suy ra, $\overline{C^{\text{'}}}\left(x\right)=-\frac{800}{x^2}+0,0002=\frac{0,0002x^2-800}{x^2}$

            $\overline{C^{\text{'}}}\left(x\right)$  = 0 ⇔ x = 2 000 (do x > 0).

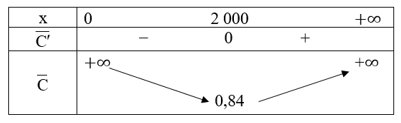
Bảng biến thiên của hàm số:

Từ bảng biến thiên suy ta với mức sản xuất là 2 000 thì chi phí trung bình cho mỗi đơn vị hàng hóa là nhỏ nhất.

Lời giải Sách bài tập Toán lớp 12 Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn hay khác:

• Bài 1.41 trang 31 SBT Toán 12 Tập 1: Bác Hưng có một hàng rào thép dài 240 m và muốn rào cánh đồng thành một thửa ruộng hình chữ nhật ....

• Bài 1.42 trang 31 SBT Toán 12 Tập 1: Doanh số bán hệ thống âm thanh nổi mới trong một khoảng thời gian dự kiến sẽ tuân theo ....

• Bài 1.43 trang 31 SBT Toán 12 Tập 1: Một chiếc hộp dạng hình hộp chữ nhật có đáy là hình vuông và có thể tích là 2 000 cm³ ....

• Bài 1.44 trang 31 SBT Toán 12 Tập 1: Một hòn đảo nhỏ cách điểm P trên bờ biển khoảng 3 km, một thị trấn ở điểm A ....

• Bài 1.45 trang 32 SBT Toán 12 Tập 1: Chứng tỏ rằng một thùng hình trụ có thể tích V cố định cần ít vật liệu sản xuất nhất ....

• Bài 1.46 trang 32 SBT Toán 12 Tập 1: Ở 0℃, sự mất nhiệt H (tính bằng Lcal/m²h, ở đây Kcal là kilocalories và 1 Kcal = 1 000 calo) ....

• Bài 1.47 trang 32 SBT Toán 12 Tập 1: Doanh thu R (USD) từ việc cho thuê x căn hộ có thể được mô hình hóa bằng hàm số ....

• Bài 1.49 trang 32 SBT Toán 12 Tập 1: a) Nếu C(x) (USD) là chi phí sản xuất x đơn vị hàng hóa, thì chi phí trung bình cho mỗi đơn vị ....

• Bài 1.50 trang 33 SBT Toán 12 Tập 1: a) Chứng tỏ rằng nếu lợi nhuận P(x) là cực đại thì doanh thu biên bằng chi phí biên ....