Một chiếc hộp dạng hình hộp chữ nhật có đáy là hình vuông và có thể tích là 2 000 cm^3

Một chiếc hộp dạng hình hộp chữ nhật có đáy là hình vuông và có thể tích là 2 000 cm. Các kích thước của chiếc hộp là bao nhiêu nếu muốn lượng vật liệu dùng để sản xuất chiếc hộp là nhỏ nhất?

Giải sách bài tập Toán 12 Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn - Kết nối tri thức

Bài 1.43 trang 31 SBT Toán 12 Tập 1: Một chiếc hộp dạng hình hộp chữ nhật có đáy là hình vuông và có thể tích là 2 000 cm³. Các kích thước của chiếc hộp là bao nhiêu nếu muốn lượng vật liệu dùng để sản xuất chiếc hộp là nhỏ nhất?

Lời giải:

Gọi x (m) là cạnh đáy của chiếc hộp.

Khi đó, ta có chiều cao của chiếc hộp là $\frac{2000}{x^2}$  (cm).

Suy ra, tổng diện tích bề mặt của chiếc hộp là:

S = 2x² + 4x.$\frac{2000}{x^2}$  = 2x² + $\frac{8000}{x}$ , x > 0.

Ta có: S' = 4x –$\frac{8000}{x^2}$  = $\frac{4x^3-8000}{x^2}$

           S' = 0 ⇔ x = 10$\sqrt[3]{2}$ .

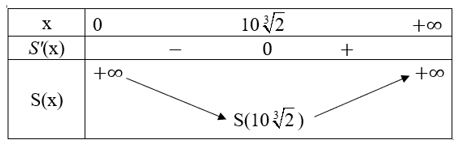
Ta có bảng biến thiên:

Dễ thấy lượng vật liệu dùng để sản xuất là nhỏ nhất khi cạnh đáy của hộp là 10$\sqrt[3]{2}$  (cm) và chiều cao của hộp là $\frac{20}{\sqrt[3]{4}}$  cm.

Lời giải Sách bài tập Toán lớp 12 Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn hay khác:

• Bài 1.41 trang 31 SBT Toán 12 Tập 1: Bác Hưng có một hàng rào thép dài 240 m và muốn rào cánh đồng thành một thửa ruộng hình chữ nhật ....

• Bài 1.42 trang 31 SBT Toán 12 Tập 1: Doanh số bán hệ thống âm thanh nổi mới trong một khoảng thời gian dự kiến sẽ tuân theo ....

• Bài 1.44 trang 31 SBT Toán 12 Tập 1: Một hòn đảo nhỏ cách điểm P trên bờ biển khoảng 3 km, một thị trấn ở điểm A ....

• Bài 1.45 trang 32 SBT Toán 12 Tập 1: Chứng tỏ rằng một thùng hình trụ có thể tích V cố định cần ít vật liệu sản xuất nhất ....

• Bài 1.46 trang 32 SBT Toán 12 Tập 1: Ở 0℃, sự mất nhiệt H (tính bằng Lcal/m²h, ở đây Kcal là kilocalories và 1 Kcal = 1 000 calo) ....

• Bài 1.47 trang 32 SBT Toán 12 Tập 1: Doanh thu R (USD) từ việc cho thuê x căn hộ có thể được mô hình hóa bằng hàm số ....

• Bài 1.48 trang 32 SBT Toán 12 Tập 1: Một công ty ước tính rằng chi phí C (USD) để sản xuất x đơn vị sản phẩm có thể được ....

• Bài 1.49 trang 32 SBT Toán 12 Tập 1: a) Nếu C(x) (USD) là chi phí sản xuất x đơn vị hàng hóa, thì chi phí trung bình cho mỗi đơn vị ....

• Bài 1.50 trang 33 SBT Toán 12 Tập 1: a) Chứng tỏ rằng nếu lợi nhuận P(x) là cực đại thì doanh thu biên bằng chi phí biên ....