Nếu C(x) (USD) là chi phí sản xuất x đơn vị hàng hóa trang 32 SBT Toán 12 Tập 1

Giải sách bài tập Toán 12 Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn - Kết nối tri thức

Bài 1.49 trang 32 SBT Toán 12 Tập 1:

a) Nếu C(x) (USD) là chi phí sản xuất x đơn vị hàng hóa, thì chi phí trung bình cho mỗi đơn vị là $\overline{C}\left(x\right)=\frac{C\left(x\right)}{x}$ . Chứng minh rằng nếu chi phí trung bình là nhỏ nhất thì chi phí biên bằng chi phí trung bình.

b) Nếu C(x) = 16 000 + 200x + 4x^3/2, hãy tìm:

(i) Chi phí, chi phí trung bình và chi phí khi sản xuất 100 đơn vị hàng hóa;

(ii) Mức sản xuất mà khi đó sẽ giảm thiểu chi phí trung bình;

(iii) Chi phí trung bình nhỏ nhất.

Lời giải:

a) Chi phí biên là: $\overline{C^{\text{'}}}\left(x\right)={\left(\frac{C\left(x\right)}{x}\right)}^{\text{'}}=\frac{C^{\text{'}}\left(x\right).x-C\left(x\right)}{x^2}=0$

Suy ra $C^{\text{'}}\left(x\right).x-C\left(x\right)=0$  hay $C^{\text{'}}\left(x\right)=\frac{C\left(x\right)}{x}$ , nói cách khác là chi phí biên bằng chi phí trung bình.

b) (i) Ta có hàm chi phí trung bình là $\overline{C}\left(x\right)=\frac{C\left(x\right)}{x}$  = $\frac{16000}{x}+200+4x^{\frac{1}{2}}$ ; hàm chi phí biên là C'(x) = 200 + 6$x^{\frac{1}{2}}$ .

Suy ra C(100) = 40 000; ; C'(100) = 260.

Vậy chi phí, chi phí trung bình và chi phí biên ở mức sản xuất 100 đơn vị hàng hóa lần lượt là  40 000 USD, 400 USD, 260 USD.

(ii) Ta có: $\overline{C^{\text{'}}}\left(x\right)=-\frac{16000}{x^2}+\frac{2}{\sqrt{x}}$

 $\overline{C^{\text{'}}}\left(x\right)$= 0  ⇔ x = 400 (do x > 0).

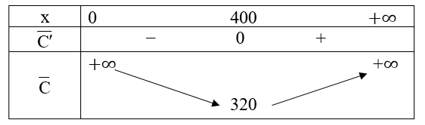
Ta có bảng biến thiên như sau:

Vậy mức sản xuất là 400 đơn vị hàng hóa sẽ giảm thiểu chi phí trung bình.

(iii) Từ bảng biến thiên ở phần b, chi phí trung bình nhỏ nhất là 320 USD.

Lời giải Sách bài tập Toán lớp 12 Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn hay khác:

• Bài 1.41 trang 31 SBT Toán 12 Tập 1: Bác Hưng có một hàng rào thép dài 240 m và muốn rào cánh đồng thành một thửa ruộng hình chữ nhật ....

• Bài 1.42 trang 31 SBT Toán 12 Tập 1: Doanh số bán hệ thống âm thanh nổi mới trong một khoảng thời gian dự kiến sẽ tuân theo ....

• Bài 1.43 trang 31 SBT Toán 12 Tập 1: Một chiếc hộp dạng hình hộp chữ nhật có đáy là hình vuông và có thể tích là 2 000 cm³ ....

• Bài 1.44 trang 31 SBT Toán 12 Tập 1: Một hòn đảo nhỏ cách điểm P trên bờ biển khoảng 3 km, một thị trấn ở điểm A ....

• Bài 1.45 trang 32 SBT Toán 12 Tập 1: Chứng tỏ rằng một thùng hình trụ có thể tích V cố định cần ít vật liệu sản xuất nhất ....

• Bài 1.46 trang 32 SBT Toán 12 Tập 1: Ở 0℃, sự mất nhiệt H (tính bằng Lcal/m²h, ở đây Kcal là kilocalories và 1 Kcal = 1 000 calo) ....

• Bài 1.47 trang 32 SBT Toán 12 Tập 1: Doanh thu R (USD) từ việc cho thuê x căn hộ có thể được mô hình hóa bằng hàm số ....

• Bài 1.48 trang 32 SBT Toán 12 Tập 1: Một công ty ước tính rằng chi phí C (USD) để sản xuất x đơn vị sản phẩm có thể được ....

• Bài 1.50 trang 33 SBT Toán 12 Tập 1: a) Chứng tỏ rằng nếu lợi nhuận P(x) là cực đại thì doanh thu biên bằng chi phí biên ....