Trên một trục số gốc O, hai điểm A và B lần lượt biểu diễn hai số nguyên a và b
Giải sách bài tập Toán lớp 6 Bài tập ôn tập cuối năm
Haylamdo biên soạn và sưu tầm lời giải Bài 5 trang 92 sách bài tập Toán lớp 6 Tập 2 sách Kết nối tri thức với cuộc sống được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 6.
Bài 5 trang 92 sách bài tập Toán lớp 6 Tập 2: Trên một trục số gốc O, hai điểm A và B lần lượt biểu diễn hai số nguyên a và b.
a) Hãy tính khoảng cách AB trong mỗi trường hợp sau đây:
• a = 3 và b = 7;
• a = −3 và b = 7;
• a = −7 và b = −3;
b) Tại sao có thể kết luận rằng ta luôn có AB = b − a nếu a < b.
HD: Với mọi trường hợp sau, hãy vẽ hình minh họa (trên trục số nằm ngang với chiều dương từ trái sang phải) và chú ý rằng điểm biểu diễn số nguyên âm nằm cách gốc O một khoảng bằng −a (chẳng hạn điểm −3 nằm cách gốc O một khoảng bằng 3 = −(−3):
• Điểm O trùng với một trong hai điểm A và B.
• Điểm O nằm giữa hai điểm A và B.
• Điểm O nằm trước (bên phải) cả hai điểm A và B.
• Điểm O nằm sau (bên trái) cả hai điểm A và B.
Lời giải:
a)
• a = 3 và b = 7
- Vẽ trục số nằm ngang gốc O.
- Hai điểm A và B lần lượt biểu diễn hai số nguyên a = 3 và b = 7.
Hai điểm A và B được biểu diễn trên trục số như hình vẽ:
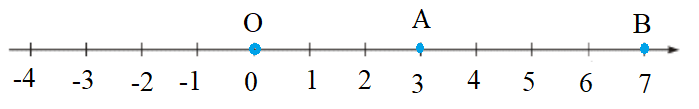
Dựa trên hình vẽ, ta có: OA = 3, OB = 7.
Khoảng cách AB:
AB = OB – OA = 7 – 3 = 4
Vậy AB = 4.
• a = −3 và b = 7
- Vẽ một trục số gốc O.
- Hai điểm A và B lần lượt biểu diễn hai số nguyên a = −3 và b = 7.
Hai điểm A và B được biểu diễn trên trục số như hình vẽ:
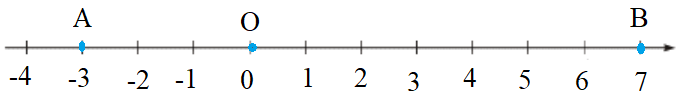
Dựa trên hình vẽ, ta có: OA = 3, OB = 7.
Khoảng cách AB:
AB = OA + OB = 3 + 7 = 10
Vậy AB = 10.
• a = −7 và b = −3
- Vẽ một trục số gốc O.
- Hai điểm A và B lần lượt biểu diễn hai số nguyên a = −7 và b = −3
Hai điểm A và B được biểu diễn trên trục số như hình vẽ:
Ta có hình vẽ:
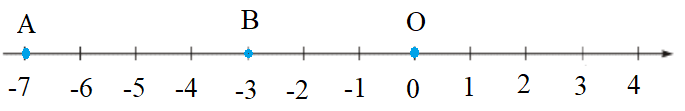
Dựa trên hình vẽ, ta có: OA = 7, OB = 3.
Khoảng cách AB:
AB = OA − OB = 7 − 3 = 4
Vậy AB = 4.
b) Hai điểm A và B lần lượt biểu diễn hai số nguyên a và b mà a < b.
Nên điểm A nằm bên trái điểm B trên trục số.
Ta xét các trường hợp sau:
• Điểm O trùng với một trong hai điểm A và B.
+ Điểm O trùng điểm A (như hình vẽ). Khi đó, a = 0.

Do đó: AB = OB = b = b – 0 = b – a.
+ Điểm O trùng điểm B. Khi đó, b = 0.

Suy ra: điểm A biểu diễn số nguyên âm nên OA = –a.
Do đó: AB = AO = OA = –a = 0 – a = b – a.
• Điểm O nằm giữa A và B.

Khi đó, điểm A biểu diễn số nguyên âm nên OA = –a;
Điểm B biểu diễn số nguyên dương nên OB = b.
Vì điểm O nằm giữa hai điểm A và B nên:
AB = OB + OA = b + (–a) = b – a.
• Điểm O nằm trước (bên phải) cả hai điểm A và B.
Mà điểm A nằm bên trái điểm B trên trục số.
Nên diểm A nằm giữa O và B (như hình vẽ).

Khi đó, hai điểm A và B đều biểu diễn số nguyên dương.
Nên OA = a, OB = b.
Ta có A nằm giữa O và B nên AO + AB = OB
Do đó: AB = OB – AO = b – a.
• Điểm O nằm sau (bên trái) cả hai điểm A và B.
Mà điểm A nằm bên trái điểm B trên trục số.
Nên điểm B nằm giữa A và O (như hình vẽ).

Khi đó, hai điểm A và B đều biểu diễn số nguyên âm.
Nên OA = –a; OB = –b.
Vì B nằm giữa A và O nên AB + BO = AO.
Do đó: AB = AO – BO = –a – (–b) = b – a .
Vậy ta có thể kết luận rằng ta luôn có AB = b – a nếu a < b.

