Cho tam giác ABC có AB lớn hơn AC Trên tia đối của tia BC lấy điểm M
Giải sách bài tập Toán lớp 7 Bài tập cuối chương 8
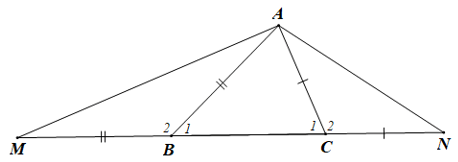
Bài 4 trang 65 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC có AB > AC. Trên tia đối của tia BC lấy điểm M sao cho BM = BA. Trên tia đối của tia CB lấy điểm N sao cho CN = CA.
a) Hãy so sánh các góc ^AMB và ^ANC.
b) Hãy so sánh các đoạn AM và AN.
Lời giải:
a) Xét ∆ABC có AB > AC (giả thiết) nên ^C1>^B1 (trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn) (1)
Vì CN = CA (giả thiết) nên tam giác ANC cân tại C.
Suy ra ^ANC=^NAC (tính chất tam giác cân).
Mặt khác ^ANC+^NAC+ˆC2=180° (tổng ba góc trong tam giác CAN).
Do đó ˆC2=180°−2^ANC
Mà ˆC1+ˆC2=180o (hai góc kề bù) nên ˆC2=180o−ˆC1
Suy ra ˆC1=2^ANC (2)
Tương tự với tam giác BAM ta có: ^B1=2^AMB (3).
Từ (1),(2),(3) suy ra ^ANC>^AMB.
Vậy ^ANC>^AMB.
b) Xét tam giác ANM có ^ANM>^AMN (do ^ANC>^AMB)
Do đó AM > AN (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn).
Vậy AM > AN.
