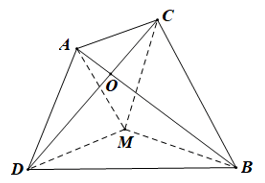
Cho hai đoạn thẳng AB và CD cắt nhau tại O Tìm điểm M sao cho: MA + MB + MC + MD nhỏ nhất

Cho hai đoạn thẳng AB và CD cắt nhau tại O. Tìm điểm M sao cho: MA + MB + MC + MD nhỏ nhất.

Giải sách bài tập Toán lớp 7 Bài tập cuối chương 8

Bài 5 trang 65 sách bài tập Toán lớp 7 Tập 2: Cho hai đoạn thẳng AB và CD cắt nhau tại O. Tìm điểm M sao cho: MA + MB + MC + MD nhỏ nhất.

Lời giải:

Xét ∆ABM có: MA + MB ≥ AB (bất đẳng thức trong tam giác)

Xét ∆CDM có: MC + MD ≥ CD (bất đẳng thức trong tam giác)

Suy ra MA + MB + MC + MD ≥ AB + CD.

Nên MA + MB + MC + MD nhỏ nhất khi và chỉ khi:

MA + MB + MC + MD = AB + CD

Khi đó MA + MB = ABvà MC + MD = CD

Điều này chỉ xảy ra khi M trùng với điểm O.

Vậy khi điểm M là giao điểm của AB và CD thì MA + MB + MC + MD nhỏ nhất.