Cho tứ giác ABCD. Chứng minh diện tích của tứ giác ABCD không lớn hơn

Cho tứ giác ABCD. Chứng minh diện tích của tứ giác ABCD không lớn hơn

Giải SBT Toán 9 Bài 1: Bất đẳng thức - Cánh diều

Bài 10 trang 37 SBT Toán 9 Tập 1: Cho tứ giác ABCD. Chứng minh diện tích của tứ giác ABCD không lớn hơn

$\frac{AB\cdot BC+AD\cdot DC}{2}\text{.}$

Lời giải:

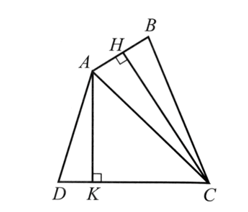
Kẻ CH vuông góc với AB tại H, AK vuông góc với CD tại K.

Khi đó, diện tích của tam giác ABC là: $S_1=\frac{AB\cdot CH}{2}$ và diện tích của tam giác ACD là: $S_2=\frac{DC\cdot AK}{2}.$

Diện tích của tứ giác ABCD là:

$S=S_1+S_2=\frac{AB\cdot CH+AK\cdot DC}{2}.$

Mà CH ≤ BC và AK ≤ AD (trong các đường xiên, đường vuông góc có độ dài ngắn nhất), suy ra $S\le \frac{AB\cdot BC+AD\cdot DC}{2}.$

Vậy diện tích của tứ giác ABCD không lớn hơn $\frac{AB\cdot BC+AD\cdot DC}{2}\text{.}$

Lời giải SBT Toán 9 Bài 1: Bất đẳng thức hay khác:

• Bài 1 trang 35 SBT Toán 9 Tập 1: Cho các số a, b, c, d đều khác 0 thoả mãn a > b và c > d. Trong các bất đẳng thức sau, bất đẳng thức nào đúng?....

• Bài 2 trang 35 SBT Toán 9 Tập 1: Cho a < b. So sánh: a) M = ‒24(a + 23) và N = ‒24(b + 23);....

• Bài 3 trang 35 SBT Toán 9 Tập 1: Cho x, y là các số thực tuỳ ý thoả mãn x > y. Bất đẳng thức x² > y² là đúng hay sai? Vì sao?....

• Bài 4 trang 35 SBT Toán 9 Tập 1: Cho a, b, c, d là các số không âm thoả mãn a > c + d, b > c + d. Chứng minh:....

• Bài 5 trang 35 SBT Toán 9 Tập 1: Cho x, y, z là các số thực tuỳ ý. Chứng minh: a) x² + y² ≥ –2xy;....

• Bài 6 trang 35 SBT Toán 9 Tập 1: Chứng minh: a) $\sqrt{5}-\sqrt{7}<\sqrt{6}-2;$....

• Bài 7 trang 36 SBT Toán 9 Tập 1: Cho a, b, c là độ dài ba cạnh của một tam giác. Chứng minh: a) a² + b² + c² < 2(ab + bc + ca);....

• Bài 8 trang 36 SBT Toán 9 Tập 1: Theo Tổng cục Môi trường, chỉ số chất lượng không khí được tính theo thang điểm (khoảng giá trị AQI) tương ứng với biểu tượng ....

• Bài 9 trang 36 SBT Toán 9 Tập 1: Một cửa hàng nhập về 60 chiếc điện thoại từ nước ngoài với giá nhập vào là 20 triệu đồng/chiếc....

• Bài 11 trang 37 SBT Toán 9 Tập 1: Bác Long dùng 80 m lưới thép gai để rào một mảnh vườn có dạng hình chữ nhật. Bác Long đã tận dụng bờ giậu có sẵn....