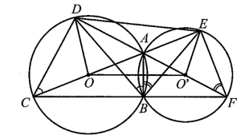
Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm phân biệt A, B
Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm phân biệt A, B. Đường thẳng AO cắt (O) và (O’) lần lượt tại hai điểm C, E (khác điểm A). Đường thẳng AO’ cắt (O) và (O’) lần lượt tại hai điểm D, F (khác điểm A). Chứng minh:
Giải SBT Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác - Cánh diều
Bài 10 trang 86 SBT Toán 9 Tập 2: Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm phân biệt A, B. Đường thẳng AO cắt (O) và (O’) lần lượt tại hai điểm C, E (khác điểm A). Đường thẳng AO’ cắt (O) và (O’) lần lượt tại hai điểm D, F (khác điểm A). Chứng minh:
a) C, B, F thẳng hàng;
b) Bốn điểm C, D, E, F cùng nằm trên một đường tròn;
c) A là tâm đường tròn nội tiếp tam giác BDE.
Lời giải:
a) Xét đường tròn (O) có AC là đường kính nên (góc nội tiếp chắn nửa đường tròn (O)).
Xét đường tròn (O’) có AF là đường kính nên (góc nội tiếp chắn nửa đường tròn (O’)).
Do đó hay
Suy ra C, B, F thẳng hàng.
b) Xét đường tròn (O) có AC là đường kính nên (góc nội tiếp chắn nửa đường tròn (O)).
Xét đường tròn (O’) có AF là đường kính nên (góc nội tiếp chắn nửa đường tròn (O’)).
Do đó nên hai điểm D, E nằm trên đường tròn đường kính CF.
Vậy bốn điểm C, D, E, F cùng nằm trên một đường tròn đường kính CF.
c) Ta có (hai góc nội tiếp cùng chắn cung DA của đường tròn (O)).
Tương tự và
Suy ra do đó BA là phân giác của góc DBE.
Tương tự, DA là phân giác của góc BDE.
Suy ra A là tâm đường tròn nội tiếp tam giác BDE.
Lời giải SBT Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác hay khác: