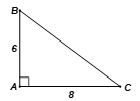
Cho tam giác ABC vuông tại A có AB = 6, AC = 8, bán kính đường tròn nội tiếp là r

Cho tam giác ABC vuông tại A có AB = 6, AC = 8, bán kính đường tròn nội tiếp là r, bán kính đường tròn ngoại tiếp là R. Tính

Giải SBT Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác - Cánh diều

Bài 8 trang 86 SBT Toán 9 Tập 2: Cho tam giác ABC vuông tại A có AB = 6, AC = 8, bán kính đường tròn nội tiếp là r, bán kính đường tròn ngoại tiếp là R. Tính $\frac{r}{R}.$

Lời giải:

Tam giác ABC vuông tại A, theo định lí Pythagore, ta có:

BC² = AB² + AC² = 6² + 8² = 100.

Suy ra $BC=\sqrt{100}=10.$

Do đó bán kính đường tròn ngoại tiếp tam giác ABC là $R=\frac{BC}{2}=\frac{10}{2}=5.$

Lại có $r=\frac{AB+AC-BC}{2}$ (theo kết quả của Ví dụ 4, trang 83, SBT Toán 9, Tập một)

Suy ra $r=\frac{AB+AC-BC}{2}=\frac{6+8-10}{2}=\frac{4}{2}=2.$

Do đó $\frac{r}{R}=\frac{2}{5}.$

Lời giải SBT Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác hay khác:

• Bài 1 trang 84 SBT Toán 9 Tập 2: Tìm phát biểu đúng trong các phát biểu sau ....

• Bài 2 trang 84 SBT Toán 9 Tập 2: Cho tam giác ABC cân tại A, có O, I lần lượt là tâm các đường tròn ngoại tiếp ....

• Bài 3 trang 85 SBT Toán 9 Tập 2: Cho tam giác ABC cân tại A, có O, I lần lượt là tâm các đường tròn ngoại tiếp ....

• Bài 4 trang 85 SBT Toán 9 Tập 2: Vẽ đường tròn (O) ngoại tiếp tam giác MNP trong các trường hợp sau ....

• Bài 5 trang 85 SBT Toán 9 Tập 2: Cho tam giác nhọn ABC. Các đường cao BE, CD của tam giác ABC cắt nhau tại K ....

• Bài 6 trang 85 SBT Toán 9 Tập 2: Cho tam giác nhọn ABC $\left(\widehat{B}>\widehat{C}\right),$ phân giác AM. Gọi O, O₁, O₂ lần lượt là tâm đường ....

• Bài 7 trang 85 SBT Toán 9 Tập 2: Trên đường tròn (O) bán kính R, lấy các điểm A, B, C, D sao cho $\text{sđ}\stackrel{⏜}{AB}=60°,$ ....

• Bài 9 trang 86 SBT Toán 9 Tập 2: Cho tam giác đều ABC nội tiếp đường tròn tâm O, bán kính R ....

• Bài 10 trang 86 SBT Toán 9 Tập 2: Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm phân biệt A, B ....

• Bài 11* trang 86 SBT Toán 9 Tập 2: Cho tam giác ABC vuông cân tại C và nội tiếp đường tròn (O; R). E là điểm tùy ý ....