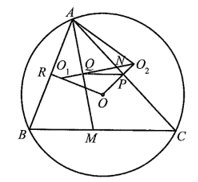
Cho tam giác nhọn ABC ( góc B > góc C ), phân giác AM. Gọi O, O1, O2 lần lượt là tâm đường tròn ngoại tiếp
Cho tam giác nhọn ABC phân giác AM. Gọi O, O, O lần lượt là tâm đường tròn ngoại tiếp các tam giác ABC, AMB, AMC. Chứng minh rằng:
Giải SBT Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác - Cánh diều
Bài 6 trang 85 SBT Toán 9 Tập 2: Cho tam giác nhọn ABC phân giác AM. Gọi O, O1, O2 lần lượt là tâm đường tròn ngoại tiếp các tam giác ABC, AMB, AMC. Chứng minh rằng:
a) OO1, OO2, O1O2 lần lượt là các đường trung trực của AB, AC, AM;
b) Tam giác OO1O2 cân.
Lời giải:
a) Do O là tâm đường tròn ngoại tiếp tam giác ABC nên OA = OB; O1 là tâm đường tròn ngoại tiếp tam giác AMB nên O1A = O1B.
Suy ra OO1 là đường trung trực của AB.
Tương tự OO2, O1O2 lần lượt là đường trung trực của AC, AM.
b) Gọi P, Q, R lần lượt là trung điểm của AC, AM, AB; N là giao điểm của QO2 và AC.
Khi đó O1Q ⊥ AM, O1R ⊥ AB nên
Tam giác AQO1 vuông tại Q nên nội tiếp đường tròn đường kính AO1.
Tam giác ARO1 vuông tại R nên nội tiếp đường tròn đường kính AO1.
Do đó tứ giác AQO1R nội tiếp đường tròn đường kính AO1.
Suy ra (tổng hai góc đối nhau của tứ giác nội tiếp bằng 180°).
Nên
Mà (hai góc kề bù) suy ra
Do đó (1)
Mặt khác, (đối đỉnh) nên
Hay (2)
Do AM là phân giác của nên hay (3)
Từ (1), (2) và (3) suy ra hay
Do đó, tam giác OO1O2 cân tại O.
Lời giải SBT Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác hay khác: