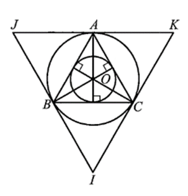
Cho tam giác đều ABC nội tiếp đường tròn tâm O, bán kính R Chứng minh rằng O cũng là tâm đường tròn

Cho tam giác đều ABC nội tiếp đường tròn tâm O, bán kính R.

Giải SBT Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác - Cánh diều

Bài 9 trang 86 SBT Toán 9 Tập 2: Cho tam giác đều ABC nội tiếp đường tròn tâm O, bán kính R.

a) Chứng minh rằng O cũng là tâm đường tròn nội tiếp tam giác ABC.

b) Vẽ tam giác IJK ngoại tiếp đường tròn (O; R) với JK // BC, IJ // AC, IK // AB. Chứng minh tam giác IJK đều.

c) Gọi R’ là bán kính của đường tròn ngoại tiếp tam giác IJK và r là bán kính của đường tròn nội tiếp tam giác ABC. Tính $\frac{r}{R^{'}} .$

Lời giải:

Cho tam giác đều ABC nội tiếp đường tròn tâm O, bán kính R Chứng minh rằng O cũng là tâm đường tròn

a) Vì O là tâm đường tròn ngoại tiếp ∆ABC nên O là trọng tâm của tam giác.

Mà trọng tâm của tam giác đều cũng là tâm đường tròn nội tiếp tam giác đều đó.

Do đó O cũng là tâm đường tròn nội tiếp tam giác ABC.

b) Do JK // BC và IK // AB nên tứ giác ABCK là hình bình hành.

Mặt khác, $\hat{A B C} = 60 °$ (do tam giác ABC đều)

Suy ra $\hat{A K C} = \hat{A B C} = 60 °$ hay $\hat{I K J} = 60 ° .$

Tương tự, ta chứng minh được $\hat{K J I} = 60 ° .$

Do đó, tam giác IJK là tam giác đều.

c) ⦁ Vì ∆IJK đều nên bán kính của đường tròn ngoại tiếp ∆IJK là $R' = \frac{J K \sqrt{3}}{3} .$

Ta có $\hat{C A K} = \hat{C K A} = 60 °$ nên ∆ACK đều nên AK = AC.

Tương tự, ta chứng minh được AJ = AB.

Lại có AB = AC (do ∆ABC đều) nên AK = AJ hay A là trung điểm của JK.

Do đó $R' = \frac{J K \sqrt{3}}{3} = \frac{2 A K \sqrt{3}}{3} = \frac{2 A C \sqrt{3}}{3} .$

⦁ Vì tam giác ABC đều nên bán kính của đường tròn nội tiếp tam giác ABC là: $r = \frac{A C \sqrt{3}}{6} .$

Suy ra $A C = \frac{6 r}{\sqrt{3}} = 2 r \sqrt{3} .$

Do đó $R' = \frac{2 \cdot 2 r \sqrt{3} \cdot \sqrt{3}}{3} = 4 r .$

Vậy $\frac{r}{R'} = \frac{1}{4} .$

Lời giải SBT Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác hay khác: