Cho tam giác ABC cân tại A, có O, I lần lượt là tâm các đường tròn ngoại tiếp

Cho tam giác ABC cân tại A, có O, I lần lượt là tâm các đường tròn ngoại tiếp và đường tròn nội tiếp tam giác ABC

Giải SBT Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác - Cánh diều

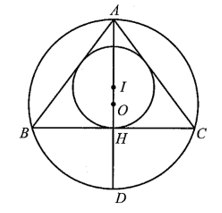
Bài 3 trang 85 SBT Toán 9 Tập 2: Cho tam giác ABC cân tại A, có O, I lần lượt là tâm các đường tròn ngoại tiếp và đường tròn nội tiếp tam giác ABC

a) Chứng minh rằng:

– Ba điểm A, O, I cùng thuộc một đường thẳng;

– Đường thẳng OA vuông góc với BC và đi qua điểm chính giữa D (khác điểm A) của cung BC.

b) Cho BC = 24 cm, AC = 20 cm. Tính độ dài bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp tam giác ABC.

Lời giải:

Cho tam giác ABC cân tại A, có O, I lần lượt là tâm các đường tròn ngoại tiếp

a) ⦁ Vì tam giác ABC cân tại A nên đường trung trực AO của cạnh BC (do O là tâm đường tròn ngoại tiếp ∆ABC) đồng thời là đường phân giác của góc BAC.

Mà AI là đường phân giác của góc BAC (do I là tâm đường tròn nội tiếp tam giác ABC).

Suy ra hai đường thẳng AO và AI trùng nhau hay ba điểm A, O, I cùng thuộc một đường thẳng.

⦁ Do OA là đường trung trực của BC nên OA ⊥ BC.

Ta có $\hat{B A I} = \hat{C A I}$ (do AI là đường phân giác của góc BAC) hay $\hat{B A O} = \hat{C A O}$

Gọi D là giao điểm của AO với đường tròn (O) (khác điểm A) nên $\hat{B A D} = \hat{C A D}$

Suy ra $\overset{⏜}{B D} = \overset{⏜}{C D} .$

Do đó đường thẳng OA đi qua điểm chính giữa D (khác điểm A) của cung BC.

b) ⦁ Gọi H là giao điểm của AD và BC. Do đó, AH ⊥ BC và H là trung điểm của BC.

Suy ra $H B = H C = \frac{1}{2} B C = \frac{1}{2} \cdot 24 = 12$ (cm).

Xét ∆ACH vuông tại H, theo định lí Pythagore, ta có:

AC² = AH² + HC²

Suy ra $A H = \sqrt{A C^{2} - H C^{2}} = \sqrt{20^{2} - 12^{2}} = \sqrt{256} = 16$ (cm).

Ta có AD là đường kính của đường tròn (O) ngoại tiếp tam giác ABC nên $\hat{A C D} = 90 ° .$

Xét ∆ACH và ∆ADC có:

$\hat{A H C} = \hat{A C D} = 90 °$ và góc A chung

Do đó ∆ACH ᔕ ∆ADC (g.g)

Suy ra $\frac{A C}{A D} = \frac{A H}{A C}$ hay AC² = AH.AD.

Nên $A D = \frac{A C^{2}}{A H} = \frac{20^{2}}{16} = 25$ (cm).

Do đó, bán kính đường tròn (O) đường kính AD ngoại tiếp ∆ABC là

$R = \frac{A D}{2} = \frac{25}{2} = 12, 5$ (cm).

⦁ Do ∆ABC cân tại A nên AB = AC = 20 cm.

Do BI là phân giác của góc ABH nên $\frac{I H}{I A} = \frac{B H}{B A} = \frac{12}{20} = \frac{3}{5} .$

Ta có $\frac{I H}{I A} = \frac{3}{5}$ hay $\frac{I H}{I H + I A} = \frac{3}{3 + 5}$ (tính chất tỉ lệ thức) hay $\frac{I H}{A H} = \frac{3}{8}$

Tức là $\frac{r}{16} = \frac{3}{8} .$ Vì vậy $r = \frac{16 \cdot 3}{8} = 6$ cm.

Vậy độ dài bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp tam giác ABC lần lượt là R = 12,5 cm và r = 6 cm.

Lời giải SBT Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác hay khác:

Xem thêm các bài giải sách bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯

SBT Toán 9 Cánh diều

Cho tam giác ABC cân tại A, có O, I lần lượt là tâm các đường tròn ngoại tiếp

Giải SBT Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác - Cánh diều

Xem thêm các bài giải sách bài tập Toán lớp 9 Cánh diều hay, chi tiết khác: