Cho tam giác nhọn ABC. Các đường cao BE, CD của tam giác ABC cắt nhau
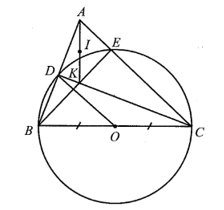
Cho tam giác nhọn ABC. Các đường cao BE, CD của tam giác ABC cắt nhau tại K. Tìm tâm đường tròn ngoại tiếp mỗi tam giác sau:
Giải SBT Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác - Cánh diều
Bài 5 trang 85 SBT Toán 9 Tập 2: Cho tam giác nhọn ABC. Các đường cao BE, CD của tam giác ABC cắt nhau tại K. Tìm tâm đường tròn ngoại tiếp mỗi tam giác sau:
a) Tam giác BDE;
b) Tam giác DEC;
c) Tam giác ADE.
Lời giải:
a) Gọi O là trung điểm của BC. Khi đó
Do BE, CD là các đường cao của tam giác ABC nên BE ⊥ AC, CD ⊥ AB.
Suy ra tam giác BDC vuông ở D và BEC vuông ở E nên
Do đó OB = OD = OC = OE nên O là tâm đường tròn ngoại tiếp tam giác BDE.
b) Do OD = OE = OC nên O là tâm đường tròn ngoại tiếp tam giác DEC.
c) Gọi I là trung điểm của AK.
Do BE ⊥ AC, CD ⊥ AB nên tam giác ADK vuông ở D và tam giác AEK vuông ở E nên khi chứng minh tương tự câu a, ta có IA = IK = IE = ID.
Do đó, I là tâm đường tròn ngoại tiếp tam giác ADE.
Lời giải SBT Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác hay khác: