Cho tứ giác ABCD nội tiếp đường tròn (O), hai tia AB, DC cắt nhau tại M

Cho tứ giác ABCD nội tiếp đường tròn (O), hai tia AB, DC cắt nhau tại M và Khi đó số đo góc BCM là:

Giải SBT Toán 9 Bài tập cuối chương 8 - Cánh diều

Bài 23 trang 92 SBT Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp đường tròn (O), hai tia AB, DC cắt nhau tại M và $\widehat{BAD}=70°.$ Khi đó số đo góc BCM là:

A. 80°.

B. 70°.

C. 110°.

D. 100°.

Lời giải:

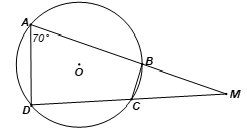
Vì ABCD nội tiếp đường tròn (O) nên tổng hai góc đối nhau bằng 180°, suy ra $\widehat{BAD}+\widehat{BCD}=180°$

Mà $\widehat{BCM}+\widehat{BCD}=180°$ (hai góc kề bù)

Nên $\widehat{BCM}=\widehat{BAD}=70°.$

Lời giải SBT Toán 9 Bài tập cuối chương 8 hay khác:

• Bài 24 trang 92 SBT Toán 9 Tập 2: Cho hình bình hành ABCD. Đường tròn đi qua ba điểm A, B, C cắt cạnh CD ở P ....

• Bài 25 trang 92 SBT Toán 9 Tập 2: Cho tam giác ABC có BC = 10 và $\widehat{BAC}=30°.$ Tính bán kính đường tròn ngoại tiếp ....

• Bài 26 trang 92 SBT Toán 9 Tập 2: Cho tứ giác ABCD có $\widehat{C}+\widehat{D}=90°.$ Gọi M, N, P, Q lần lượt là trung điểm của AB, BD, DC, CA ....

• Bài 27 trang 92 SBT Toán 9 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH = 2,4 cm và ....

• Bài 28 trang 92 SBT Toán 9 Tập 2: Đường tròn tâm I nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại F và E ....

• Bài 29 trang 93 SBT Toán 9 Tập 2: Cho tam giác ABC nhọn. Ba đường cao AI, BK, CL. Chứng minh ....

• Bài 30 trang 93 SBT Toán 9 Tập 2: Quan sát Hình 16 ....

• Bài 31 trang 93 SBT Toán 9 Tập 2: Cho lục giác đều ABCDEF cạnh bằng a ....

• Bài 32 trang 93 SBT Toán 9 Tập 2: Cho đường tròn (O; R). Từ điểm M nằm ngoài đường tròn (O; R), kẻ các tiếp tuyến ....

• Bài 33* trang 93 SBT Toán 9 Tập 2: Cho đường tròn (I; r) cố định. Một tam giác ABC thay đổi, có chu vi bằng 16 cm ....