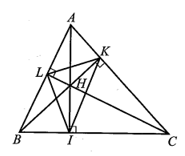
Cho tam giác ABC nhọn. Ba đường cao AI, BK, CL. Chứng minh Các tứ giác AKIB, BLKC là các tứ giác nội tiếp
Cho tam giác ABC nhọn. Ba đường cao AI, BK, CL. Chứng minh:
Giải SBT Toán 9 Bài tập cuối chương 8 - Cánh diều
Bài 29 trang 93 SBT Toán 9 Tập 2: Cho tam giác ABC nhọn. Ba đường cao AI, BK, CL. Chứng minh:
a) Các tứ giác AKIB, BLKC là các tứ giác nội tiếp;
b) Trực tâm H của tam giác ABC là tâm đường tròn nội tiếp tam giác IKL.
Lời giải:
a) Xét ∆ABC có ba đường cao AI, BK, CL nên AI ⊥ BC, BK ⊥ AC, CL ⊥ AB.
Do ∆ABK vuông tại K và ∆ABI vuông tại I nên hai điểm K, I cùng thuộc đường tròn đường kính AB. Do đó tứ giác AKIB nội tiếp đường tròn đường kính AB.
Do ∆BCL vuông tại L và ∆BCK vuông tại K nên hai điểm L, K cùng thuộc đường tròn đường kính BC. Do đó tứ giác BLKC nội tiếp đường tròn đường kính BC.
b) Do tứ giác AKIB nội tiếp đường tròn nên tổng hai góc đối nhau của tứ giác này bằng 180°, suy ra
Mà (hai góc kề bù)
Nên hay
Tương tự ta cũng có
Suy ra
Từ đó ta có hay
Vì vậy KH là đường phân giác của góc LKI.
Tương tự cũng có LH là đường phân giác của góc KLI.
Vậy H là tâm đường tròn nội tiếp tam giác IKL.
Lời giải SBT Toán 9 Bài tập cuối chương 8 hay khác: