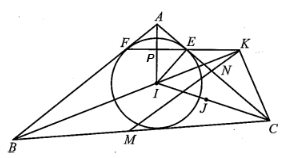
Đường tròn tâm I nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại F và E
Đường tròn tâm I nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại F và E. Kẻ CK vuông góc với BI. Gọi M, N lần lượt là trung điểm của BC, AC. Chứng minh:
Giải SBT Toán 9 Bài tập cuối chương 8 - Cánh diều
Bài 28 trang 92 SBT Toán 9 Tập 2: Đường tròn tâm I nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại F và E. Kẻ CK vuông góc với BI. Gọi M, N lần lượt là trung điểm của BC, AC. Chứng minh:
a) F, E, K thẳng hàng;
b) K, N, M thẳng hàng.
Lời giải:
a) ⦁ Gọi J là trung điểm của IC.
Vì đường tròn (I) tiếp xúc với AC tại E nên IE ⊥ AC tại E. Do đó nên điểm E thuộc đường tròn tâm J, đường kính IC.
Vì CK ⊥ BI tại K nên hay nên điểm K thuộc đường tròn tâm J, đường kính IC.
Do đó bốn điểm I, E, K, C cùng thuộc đường tròn tâm J, đường kính IC.
Như vậy, tứ giác IEKC nội tiếp đường tròn.
Suy ra (hai góc nội tiếp cùng chắn cung KC). (3)
⦁ Vì đường tròn (I) là đường tròn nội tiếp tam giác ABC nên AI, BI, CI là các đường phân giác của tam giác ABC.
Gọi P là giao điểm của AI và EF.
Do AI là tia phân giác của góc BAC nên
Do BI là tia phân giác của góc ABC nên
Do CI là tia phân giác của góc ACB nên
Vì đường tròn (I) tiếp xúc với AB, AC lần lượt tại F và E hay AE, AF là hai tiếp tuyến của đường tròn (I), do đó IE = IF và AE = AF.
Suy ra AI là đường trung trực của đoạn thẳng EF nên AI ⊥ EF tại P.
Xét ∆APE có
Suy ra
Do đó (1)
Xét ∆IBC có là góc ngoài của tam giác tại đỉnh I nên
(2)
Từ (1) và (2), suy ra (4)
Từ (3) và (4), suy ra
Mà (hai góc kề bù) nên hay
Vậy ba điểm F, E, K thẳng hàng.
b) Xét ∆KBC vuông tại K có KM là đường trung tuyến ứng với cạnh huyền BC nên
Mà M là trung điểm của BC nên
Do đó MB = MK nên ∆MKB cân ở M, suy ra
Xét ∆MKB có là góc ngoài tại đỉnh M nên
Xét ∆ABC có M, N lần lượt là trung điểm của BC, AC nên MN là đường trung bình của ∆ABC, suy ra MN // AB, do đó
Suy ra vì vậy ba điểm K, N, M thẳng hàng.
Lời giải SBT Toán 9 Bài tập cuối chương 8 hay khác: