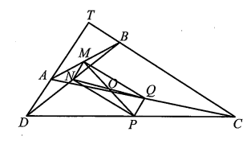
Cho tứ giác ABCD có góc C + góc D = 90 độ. Gọi M, N, P, Q lần lượt là trung điểm của AB, BD, DC, CA
Cho tứ giác ABCD có . Gọi M, N, P, Q lần lượt là trung điểm của AB, BD, DC, CA. Chứng minh bốn điểm M, N, P, Q cùng thuộc một đường tròn. Tìm tâm đường tròn đó.
Giải SBT Toán 9 Bài tập cuối chương 8 - Cánh diều
Bài 26 trang 92 SBT Toán 9 Tập 2: Cho tứ giác ABCD có . Gọi M, N, P, Q lần lượt là trung điểm của AB, BD, DC, CA. Chứng minh bốn điểm M, N, P, Q cùng thuộc một đường tròn. Tìm tâm đường tròn đó.
Lời giải:
Gọi T là giao điểm của hai đường thẳng AD và CB.
Xét ∆TCD có
Suy ra nên AD ⊥ BC.
Xét ∆ABD có M, N lần lượt là trung điểm của AB, BD nên MN là đường trung bình của ∆ABD, do đó MN // AD.
Tương tự, ta có MQ là đường trung bình của ∆ABC nên MQ // BC.
Mặt khác AD ⊥ BC, suy ra MN ⊥ MQ.
Chứng minh tương tự ta cũng có MN ⊥ NP, NP ⊥ PQ.
Suy ra MNPQ là hình chữ nhật (tứ giác có ba góc vuông).
Vậy bốn điểm M, N, P, Q cùng thuộc một đường tròn có tâm O là giao điểm của hai đường chéo MP và NQ.
Lời giải SBT Toán 9 Bài tập cuối chương 8 hay khác: