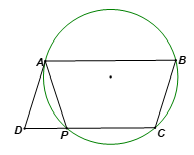
Cho hình bình hành ABCD. Đường tròn đi qua ba điểm A, B, C cắt cạnh CD ở P
Cho hình bình hành ABCD. Đường tròn đi qua ba điểm A, B, C cắt cạnh CD ở P (P khác C và D). Tìm phát biểu sai:
Giải SBT Toán 9 Bài tập cuối chương 8 - Cánh diều
Bài 24 trang 92 SBT Toán 9 Tập 2: Cho hình bình hành ABCD. Đường tròn đi qua ba điểm A, B, C cắt cạnh CD ở P (P khác C và D). Tìm phát biểu sai:
A. AP = AD.
B. Tứ giác ABCP là hình thang cân.
C.
D.
Lời giải:
Đáp án đúng là: D
– Vì bốn điểm A, B, C, P cùng nằm trên một đường tròn nên tứ giác ABCP nội tiếp, do đó tổng hai góc đối nhau của tứ giác này bằng 180°, suy ra:
⦁ Do đó phương án D là sai.
⦁ mà (hai góc kề bù)
Nên Do đó phương án C là đúng.
– Vì ABCD là hình bình hành nên AB // CD, do đó (hai góc so le trong)
Suy ra
Tứ giác ABCP có AB // CP nên là hình thang, lại có nên ABCP là hình thang cân. Do đó phương án B là đúng.
– Vì ABCP là hình thang cân nên AP = BC (hai cạnh bên bằng nhau)
Lại có AD = BC (do ABCD là hình bình hành)
Suy ra AP = AD. Do đó phương án A là đúng.
Vậy ta chọn phương án D.
Lời giải SBT Toán 9 Bài tập cuối chương 8 hay khác: